
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)构造$t(x)=\frac{{f(x)+f({x_2})}}{2}-f({\frac{{x+{x_2}}}{2}}),x∈(0,+∞)$,求出t(x)的导数,解关于导函数的不等式,得到函数的单调区间,根据函数的单调性证明即可.
解答 解:(1)$g(x)=f(x)-{x^2}=\frac{2}{x}+alnx$,∴$g'(x)=-\frac{2}{x^2}+\frac{a}{x}=\frac{ax-2}{x^2}(x>0)$.
①当a≤0时,g'(x)<0,g(x)在(0,+∞)为减函数;
②当a>0时,$g'(x)=\frac{{a(x-\frac{2}{a})}}{x^2}$,
当$0<x<\frac{2}{a}$时,g'(x)<0,g(x)为减函数;
当$x>\frac{2}{a}$时,g'(x)>0,g(x)为增函数.
∴当a>0时,g(x)在$(0,\frac{2}{a})$上为减函数,g(x)在$(\frac{2}{a},+∞)$上为增函数.
(2)证明:以x1为自变量,构造$t(x)=\frac{{f(x)+f({x_2})}}{2}-f({\frac{{x+{x_2}}}{2}}),x∈(0,+∞)$.
∴$t'(x)=\frac{1}{2}f'(x)-\frac{1}{2}\frac{{f(x+{x_2})}}{2}$,又$f'(x)=2x-\frac{2}{x^2}+\frac{a}{x}$,
$t'(x)=x-\frac{1}{x^2}+\frac{a}{2x}-\frac{1}{2}[(x+{x_2})-\frac{8}{{{{(x+{x_2})}^2}}}+\frac{2a}{{x+{x_2}}}]$=$(x-{x_2})[\frac{1}{2}+\frac{{3x+{x_2}}}{{{x^2}{{(x+{x_2})}^2}}}-\frac{a}{{2x(x+{x_2})}}]$,
∵$\frac{1}{2}>0,\frac{{3x+{x_2}}}{{{x^2}{{(x+{x_2})}^2}}}>0,-\frac{a}{{2x(x+{x_2})}}>0$,∴$\frac{1}{2}+\frac{{3x+{x_2}}}{{{x^2}{{(x+{x_2})}^2}}}-\frac{a}{{2x(x+{x_2})}}>0$.
故当x∈(0,x2)时,t'(x)<0,t(x)为减函数;
当x∈(x2,+∞)时,t'(x)>0,t(x)为增函数.
故对一切x∈(0,+∞),t(x)≥t(x2)=0.当且仅当x=x2时取等号.
题中x1≠x2,故t(x1)>0恒成立.得证.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,转化思想,考查不等式的证明,是一道综合题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [$\frac{π}{6}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
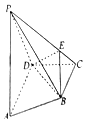 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
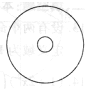 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{49}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
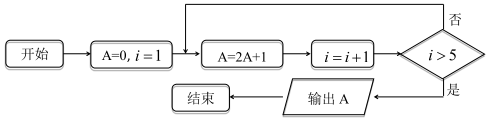
| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com