练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
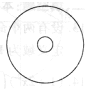
    12．如图，半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆，现将半径为1cm的一枚硬币抛到此纸板上，使整块硬币完全随机落在纸板内，则硬币与小圆无公共点的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{21}{25}$C．$\frac{1}{4}$D．$\frac{3}{4}$

    分析 由题意可得，硬币要落在纸板内，硬币圆心距离纸板圆心的距离应该小于4，硬币与小圆无公共点，硬币圆心距离小圆圆心要大于2，先求出硬币落在纸板上的面积，然后再求解硬币落下后与小圆没交点的区域的面积，代入古典概率的计算方式可求．

    解答 解：记“硬币落下后与小圆无公共点”为事件A，
    硬币要落在纸板内，硬币圆心距离纸板圆心的距离应该小于4，其面积为16π，
    无公共点也就意味着，硬币的圆心与纸板的圆心相距超过2cm，以纸板的圆心为圆心，作一个半径2cm的圆，
    硬币的圆心在此圆外面，则硬币与半径为1cm的小圆无公共交点．
    所以有公共点的概率为$\frac{4}{16}$，
    无公共点的概率为P（A）=1-$\frac{4}{16}$=$\frac{3}{4}$，
    故选：D．

    点评 本题主要考查了几何概率的计算公式，用到的知识点为：概率=相应的面积与总面积之比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．设△ABC的内角A，B，C的对边分别为a，b，c，若cosA=$\frac{3}{5}$，sinB=$\frac{{\sqrt{2}}}{2}$，a=8，则c=7$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设T?R，若存在常数M＞0，使得对任意t∈T，均有|t|≤M，则称T为有界集合，同时称M为集合T的上界．
    （1）设A1={y|y=$\frac{{2}^{x}-1}{{2}^{x}+1}$，x∈R}，A2={x|sinx＞$\frac{1}{2}$}，试判断A1、A2是否为有界集合，并说明理由；
    （2）已知f（x）=x2+u，记f1（x）=f（x），fn（x）=f（fn-1（x））（n=2，3，…），若m∈R，u∈[$\frac{1}{4}$，+∞），且B={fn（m）|n∈N*}为有界集合，求u的值及m的取值范围；
    （3）设a，b，c均为正数，将（a-b）2、（b-c）2、（c-a）2中的最小值记为d，是否存在正数λ∈（0，1），使得λ为有界集合C={y|$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$，a、b、c均为正数}的上界，若存在，试求λ的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=ax2+（1-2a）x-lnx（a∈R）．
    （1）求函数f（x）在区间[1，2]上的最大值；
    （2）若A（x1，y1），B（x2，y2），C（x0，y0）是函数f（x）图象上不同的三点，且x0=$\frac{{{x_1}+{x_2}}}{2}$，试判断f′（x0）与$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$之间的大小关系，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知平面α⊥平面β，直线m，n均不在平面α、β内，且m⊥n，则（　　）
    A．若m⊥β，则n∥βB．若n∥β，则m⊥βC．若m⊥β，则n⊥βD．若n⊥β，则m⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=x2+$\frac{2}{x}$+alnx（x＞0，a为常数）．
    （1）讨论函数g（x）=f（x）-x2的单调性；
    （2）对任意两个不相等的正数x1、x2，求证：当a≤0时，$\frac{{f（{x_1}）+f（{x_2}）}}{2}＞f（{\frac{{{x_1}+{x_2}}}{2}}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且（c+b）（sinC-sinB）=a（sinA-sinB）．若c=2$\sqrt{3}$，则a2+b2的取值范围是（20，24]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=xlnx-mx的图象与直线y=-1相切．
    （Ⅰ）求m的值，并求f（x）的单调区间；
    （Ⅱ）若g（x）=ax3，设h（x）=f（x）-g（x），讨论函数h（x）的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，且过点M（4，1）．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若直线l：y=x+m（m≠-3）与椭圆C交于P，Q两点，记直线MP，MQ的斜率分别为k1，k2，试探究k1+k2是否为定值．若是，请求出该定值；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案