
分析 由已知利用正弦定理,余弦定理可求C的值,进而由正弦定理可得a=4sinA,b=4sinB,令A=60°+α,B=60°-α,(0°≤α<30°),利用三角函数恒等变换的应用化简可得a2+b2=16(1+$\frac{1}{2}$cos2α)的值,由范围0°≤2α<60°,利用余弦函数的图象和性质可求其取值范围.
解答 解:∵(c+b)(sinC-sinB)=a(sinA-sinB).若c=2$\sqrt{3}$,
∴由正弦定理$(c+b)(c-b)=a(a-b)⇒{c^2}={a^2}+{b^2}-ab⇒cosC=\frac{1}{2}⇒C=60°⇒A+B=120°$.
∴由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=2R=\frac{c}{sinC}=\frac{{2\sqrt{3}}}{sin60°}=4⇒a=4sinA,b=4sinB$,
令A=60°+α,B=60°-α,(0°≤α<30°),
∴a2+b2=16(sin2A+sin2B)=16[sin2(60°+α)+sin2(60°-α)]
=16[($\frac{\sqrt{3}}{2}$cos$α+\frac{1}{2}sinα$)2+($\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα)2]
=16($\frac{3}{2}$cos2α+$\frac{1}{2}$sin2α)=16($\frac{3}{2}$×$\frac{1+cos2α}{2}$+$\frac{1}{2}×\frac{1-cos2α}{2}$)=16(1+$\frac{1}{2}$cos2α),
∵0°≤2α<60°,
∴$\frac{1}{2}<cos2α≤1$,
∴从而有20<a2+b2≤24.
故答案为:(20,24].
点评 本题主要考查了正弦定理,三角函数恒等变换的应用在解三角形中的应用,考查了转化思想和数形结合思想的应用,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
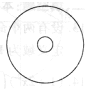 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
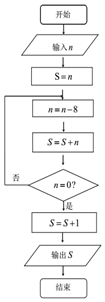 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
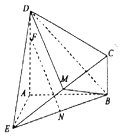 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com