
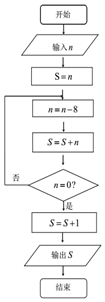
 �������㾭�����й��Ŵ���Ҫ����ѧ������Լ�������ġ������ͣ�Ҳ���Ǵ�Լһǧ�����ǰ�������ġ������㾭����������������һ���⣺�����з���һ��������һ������ʮ��ö���ʻ����Σ����������������һ�ֽ��������ķ����������ö�λ����λ���ˣ������λ���������һ�����ã���ͨ���Ը�����о����֣���һ����������һ�ѵ�ö��n��8��������ʱ�����ɲ��ô˷�����⣮��ͼ���ǽ����������ij����ͼ��������n=40��������Ľ��Ϊ121��
�������㾭�����й��Ŵ���Ҫ����ѧ������Լ�������ġ������ͣ�Ҳ���Ǵ�Լһǧ�����ǰ�������ġ������㾭����������������һ���⣺�����з���һ��������һ������ʮ��ö���ʻ����Σ����������������һ�ֽ��������ķ����������ö�λ����λ���ˣ������λ���������һ�����ã���ͨ���Ը�����о����֣���һ����������һ�ѵ�ö��n��8��������ʱ�����ɲ��ô˷�����⣮��ͼ���ǽ����������ij����ͼ��������n=40��������Ľ��Ϊ121�� ���� ģ���������У�����д��ÿ��ѭ���õ���n��S��ֵ����n=0ʱ�����������˳�ѭ�������ɵõ������Sֵ��
��� �⣺ģ���������У��ɵ�
n=40��S=40
ִ��ѭ���壬n=32��S=72
����������n=0��ִ��ѭ���壬n=24��S=96
����������n=0��ִ��ѭ���壬n=16��S=112
����������n=0��ִ��ѭ���壬n=8��S=120
����������n=0��ִ��ѭ���壬n=0��S=120
��������n=0���ɵ�S=121���˳�ѭ�������S��ֵΪ121��
�ʴ�Ϊ��121��
���� ���⿼���֪ʶ����ѭ���ṹ�ij����ͼ��Ӧ�ã���д��������н��ʱ�����dz�ʹ��ģ��ѭ���ı䷨���������ѭ�����б����Ƚ϶�ʱ��Ҫ�ñ������ݽ��й��������ڻ����⣮


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�ͦ£���n�Φ� | B�� | ��n�Φ£���m�ͦ� | C�� | ��m�ͦ£���n�ͦ� | D�� | ��n�ͦ£���m�ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{3}{2}$ | C�� | $\frac{12}{5}$ | D�� | $\frac{13}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
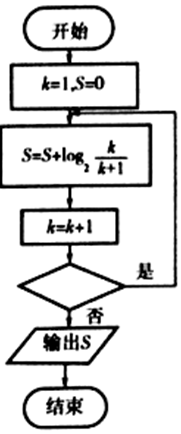
| A�� | k��2 | B�� | k��3 | C�� | k��4 | D�� | k��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-�ޣ�-\frac{1}{e}-2e}��$ | B�� | $��{-�ޣ�\frac{1}{e}-e}��$ | C�� | $��{\frac{1}{e}+2e��+��}��$ | D�� | $��{\frac{1}{e}+e��+��}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com