
分析 (Ⅰ)an+1=2an+4,变形为an+1+4=2(an+4),利用等比数列的通项公式即可得出.
( II)由(Ⅰ)可知,${a_n}={2^n}-4$,利用等比数列的求和公式即可得出.
解答 解:(Ⅰ)证明:an+1=2an+4,变形为an+1+4=2(an+4).--------------(2分)
又∵a1=-2,∴a1+4=2∴数列{an+4}为以2为首项,2为公比的等比数列--------------(4分)∴${a_n}+4={2^n},{a_n}={2^n}-4$-------------(6分)
( II)由(Ⅰ)可知,${a_n}={2^n}-4$
∴Sn=2+22+…+2n-4n,------------------------(9分)
=$\frac{{2({1-{2^n}})}}{1-2}-4n={2^{n+1}}-4n-2$------------------------(12分)
点评 本题考查了等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
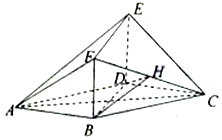 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
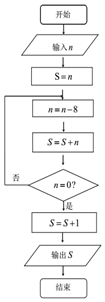 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 安全感指数 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100] |
| 男居民人数 | 8 | 16 | 226 | 131 | 119 |
| 女居民人数 | 12 | 14 | 174 | 122 | 178 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
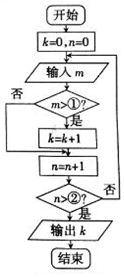 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )| A. | 14,19 | B. | 14,20 | C. | 15,19 | D. | 15,20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com