练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
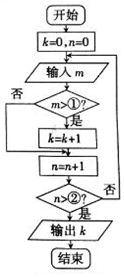
    18．现有若干（大于20）件某种自然生长的中药材，从中随机抽取20件，其重量都精确到克，规定每件中药材重量不小于15克为优质品．如图所示的程序框图表示统计20个样本中的优质品，其中m表示每件药材的重量，则图中①，②两处依次应该填的整数分别是（　　）
    A．14，19B．14，20C．15，19D．15，20

    分析 要统计20个样本中的优质品数，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解答 解：由题意，模拟程序的运行，可得：
    要统计20个样本中的优质品数，每件中药材重量不小于15克为优质品．
    故当m＞14时，执行循环体，k=k+1，计数器k的值加1，
    当n=19时，输入了20个m的值，故当n＞19时，退出循环，输出k的值．
    故①，②两处依次应该填的整数分别是14，19．
    故选：A．

    点评 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知数列{an}满足a1=-2，an+1=2an+4．
    （ I）求证{an+4}是等比数列，并求数列{an}的通项公式；
    （ II）求数列{an}的前n项的和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合A={x|y=log2（3-x）}，B={x||2x-1|＞1}，则A∩B=（　　）
    A．{x|1＜x＜3}B．{x|-1＜x＜3}C．{x|x＜0或0＜x＜3}D．{x|x＜0或1＜x＜3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知f（x）=|xex|，又g（x）=[f（x）]2-tf（x）（t∈R），若方程g（x）=-2有4个不同的根，则t的取值范围为（　　）
    A．$（{-∞，-\frac{1}{e}-2e}）$B．$（{-∞，\frac{1}{e}-e}）$C．$（{\frac{1}{e}+2e，+∞}）$D．$（{\frac{1}{e}+e，+∞}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知a＜b＜0，则（　　）
    A．$\frac{1}{a}＜\frac{1}{b}$B．a2＜abC．a2＜b2D．$\frac{1}{a-b}＜\frac{1}{a}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=xex．
    （Ⅰ）讨论函数g（x）=af（x）+ex的单调性；
    （Ⅱ）若直线y=x+2与曲线y=f（x）的交点的横坐标为t，且t∈[m，m+1]，求整数m所有可能的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率e=$\sqrt{2}$，且它的一个顶点到较近焦点的距离为$\sqrt{2}$-1，则双曲线C的方程为x2-y2=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．执行如图所示的程序框图，则输出i的值为（　　）
    A．1006B．1007C．1008D．1009

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某高中组织数学知识竞赛，采取答题闯关的形式，分两种题型，每种题型设两关．“数学文化”题答对一道得5分，“数学应用”题答对一道得10分，答对一道题即可进入下一关，否则终止比赛．有甲、乙、丙三人前来参赛，设三人答对每道题的概率分别是$\frac{3}{4}$、$\frac{2}{3}$、$\frac{1}{2}$，三人答题互不影响．甲、乙选择“数学文化”题，丙选择“数学应用”题．
    （Ⅰ）求乙、丙两人所得分数相等的概率；
    （Ⅱ）设甲、丙两人所得分数之和为随机变量X，求X的分布列与期望．

    查看答案和解析>>

    同步练习册答案