
| A. | $({-∞,-\frac{1}{e}-2e})$ | B. | $({-∞,\frac{1}{e}-e})$ | C. | $({\frac{1}{e}+2e,+∞})$ | D. | $({\frac{1}{e}+e,+∞})$ |
分析 设f(x)=λ,研究f(x)的单调性和极值,得出f(x)=λ的解的情况,从而确定关于λ的方程λ2-tλ+2=0的解的分布情况,利用二次函数的性质得出t的范围.
解答 解:解:f(x)=$\left\{\begin{array}{l}{x{e}^{x},x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,
当x≥0时,f′(x)=ex+xex=(1+x)ex>0,
∴f(x)在[0,+∞)上是增函数,
当x<0时,f′(x)=-ex-xex=(-1-x)ex,
∴当x<-1时,f′(x)>0,当-1<x<0时,f′(x)<0,
∴f(x)在(-∞,-1]上是增函数,在(-1,0)上是减函数.
当x=-1时,f(x)取得极大值f(-1)=$\frac{1}{e}$.
令f(x)=λ,
又f(x)≥0,f(0)=0,
则当λ<0时,方程f(x)=λ无解;
当λ=0或λ>$\frac{1}{e}$时,方程f(x)=λ有一解;
当λ=$\frac{1}{e}$时,方程f(x)=λ有两解;
当0<λ<$\frac{1}{e}$时,方程f(x)=λ有三解.
∵方程g(x)=-2有4个不同的根,即[f(x)]2-tf(x)+2=0有4个不同的解,
∴关于λ的方程λ2-tλ+2=0在(0,$\frac{1}{e}$)和($\frac{1}{e}$,+∞)上各有一解.
∴$\left\{\begin{array}{l}{{t}^{2}-8>0}\\{\frac{1}{{e}^{2}}-\frac{t}{e}+2<0}\end{array}\right.$,解得t>$\frac{1}{e}+2e$.
故选C.
点评 本题考查了函数的零点个数与单调性和极值的关系,二次函数的性质,换元法解题思想,属于中档题.


科目:高中数学 来源: 题型:填空题
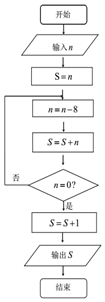 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
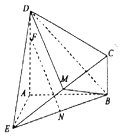 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
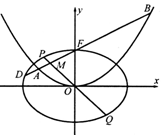 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
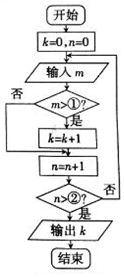 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )| A. | 14,19 | B. | 14,20 | C. | 15,19 | D. | 15,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com