
分析 (I)利用二倍角和诱导公式以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,图象上相邻的最高点和最低点的距离为$\sqrt{5}$.求出相邻的最高点和最低点横坐标的距离就是$\frac{1}{2}T$,可得T的值,从而求出ω.可得f(x)的解析式及对称中心;
(II)x∈$[{-1,\frac{1}{2}}]$上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值,即得到f(x)的取值范围.
解答 解:(I)函数f(x)=$\sqrt{3}sinωxsin({\frac{π}{2}-ωx})-{cos^2}ωx+\frac{1}{2}({ω>0})$,
化简可得:f(x)=$\sqrt{3}$sinωxcosωx-$\frac{1}{2}$-$\frac{1}{2}$cos2ωx+$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx=sin(2ωx-$\frac{π}{6}$)
设函数f(x)的最小正周期为T,
∵图象上相邻的最高点和最低点的距离为$\sqrt{5}$.相邻的最高点和最低点纵坐标的差为2.
∴相邻的最高点和最低点横坐标的距离为$\frac{1}{2}T$=5-4
∴T=2,即$\frac{2π}{2ω}=2$,
∴ω=$\frac{π}{2}$.
则f(x)的解析式为:f(x)=sin(πx-$\frac{π}{6}$)
令πx-$\frac{π}{6}$=kπ,k∈Z,
可得:x=k$+\frac{1}{6}$.
∴f(x)的对称中心为($k+\frac{1}{6},0$),k∈Z;
(II)x∈$[{-1,\frac{1}{2}}]$上时,
可得:$-\frac{7π}{6}≤πx-\frac{π}{6}≤\frac{π}{3}$,
当πx-$\frac{π}{6}$=$-\frac{π}{2}$时,函数f(x)取得最小值为-1.
当πx-$\frac{π}{6}$=$\frac{π}{3}$时,函数f(x)取得最大值为$\frac{\sqrt{3}}{2}$.
∴函数f(x)在$[{-1,\frac{1}{2}}]$上的最小值为-1.最大值为$\frac{\sqrt{3}}{2}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{e}-2e})$ | B. | $({-∞,\frac{1}{e}-e})$ | C. | $({\frac{1}{e}+2e,+∞})$ | D. | $({\frac{1}{e}+e,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
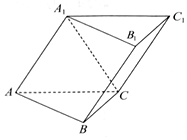 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1•d<0 | B. | |Sn|有最小值 | ||
| C. | ${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$>0 | D. | ${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 9 | B. | -6 27 | C. | -12 9 | D. | -12 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
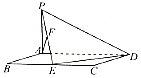 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com