
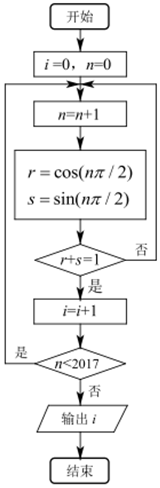
 执行如图所示的程序框图,则输出i的值为( )
执行如图所示的程序框图,则输出i的值为( )| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
分析 模拟程序的运行,根据判断框的功能,依次写出每次循环得到的i的值,观察规律即可得解.
解答 解:模拟程序的运行,由正弦函数,余弦函数的取值规律可得:
当n=1,满足条件r+s=1,i=1
n=2,不满足条件r+s=1,
n=3,不满足条件r+s=1,
n=4,满足条件r+s=1,i=2
n=5,不满足条件r+s=1,
…
观察规律可得,当n=4k(k为整数)时,i的值为2k,由于2017=504×4+1,
可得:当n=2016时,i的值为504×2=1008,
满足条件n<2017,满足条件r+s=1,i=1009,
此时,不满足条件n<2017,退出循环,输出i的值为1009.
故选:D.
点评 本题主要考查了循环结构的程序框图的应用,模拟程序的运行得到i的取值规律是解题的关键,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
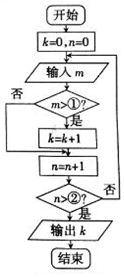 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )| A. | 14,19 | B. | 14,20 | C. | 15,19 | D. | 15,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com