
Ζ÷Έω Θ®1Θ©‘≠ΖΫ≥Χ±δ–ΈΈΣΠ―2sin2Π»=Π―cosΠ»Θ§άϊ”ΟΜΞΜ·ΙΪ ΫΩ…ΒΟΘΚCΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ°
Θ®2Θ©Α―lΒΡΖΫ≥Χ¥ζ»κy2=xΒΟt2sin2ΠΝ-tcosΠΝ-1=0Θ§άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒΦΑΤδ“―÷ΣΩ…ΒΟΘΚ|t1-t2|=2|t1t2|Θ§ΤΫΖΫΒΟ${Θ®{{t_1}+{t_2}}Θ©^2}-4{t_1}{t_2}=4t_1^2t_2^2$Θ§Ω…ΒΟsin2ΠΝ=1Θ§Φ¥Ω…ΒΟ≥ωΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©‘≠ΖΫ≥Χ±δ–ΈΈΣΠ―2sin2Π»=Π―cosΠ»Θ§
ΓΏx=Π―cosΠ»Θ§y=Π―sinΠ»Θ§
ΓύCΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΈΣy2=xΘ§ΤδΫΙΒψΈΣ$FΘ®{\frac{1}{4}Θ§0}Θ©$Θ°
Θ®2Θ©Α―lΒΡΖΫ≥Χ¥ζ»κy2=xΒΟt2sin2ΠΝ-tcosΠΝ-1=0Θ§
‘ρ${t_1}+{t_2}=\frac{cosΠΝ}{{{{sin}^2}ΠΝ}}Θ§{t_1}{t_2}=-\frac{1}{{{{sin}^2}ΠΝ}}$Θ§ΔΌ
$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}=2?|{PA}|+|{PB}|=2|{PA}|•|{PB}|$Θ§
Φ¥|t1-t2|=2|t1t2|Θ§
ΤΫΖΫΒΟ${Θ®{{t_1}+{t_2}}Θ©^2}-4{t_1}{t_2}=4t_1^2t_2^2$Θ§ΔΎ
Α―ΔΌ¥ζ»κΔΎΒΟ$\frac{{{{cos}^2}ΠΝ}}{{{{sin}^4}ΠΝ}}+\frac{4}{{{{sin}^2}ΠΝ}}=\frac{4}{{{{sin}^4}ΠΝ}}$Θ§Γύsin2ΠΝ=1Θ§
ΓΏΠΝ «÷±œΏlΒΡ«ψ–±Ϋ«Θ§Γύ$ΠΝ=\frac{Π–}{2}$Θ§
ΓύlΒΡΤ’Ά®ΖΫ≥ΧΈΣx=1Θ§«“|AB|=2Θ§
ΒψFΒΫABΒΡΨύάκd=1-$\frac{1}{4}$=$\frac{3}{4}$
ΓύΓςFABΒΡΟφΜΐΈΣS=$\frac{1}{2}$|AB|ΓΝd=$\frac{1}{2}ΓΝ2ΓΝ\frac{3}{4}$=$\frac{3}{4}$Θ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ιΦΪΉχ±ξœΒ”κ≤Έ ΐΖΫ≥ΧΒΡœύΙΊ÷Σ ΕΓΔΦΪΉχ±ξΖΫ≥Χ”κΤΫΟφ÷±Ϋ«Ήχ±ξΖΫ≥ΧΒΡΜΞΜ·ΓΔ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΒΡΙΊœΒΘ§ΩΦ≤ιΝΥΆΤάμΡήΝΠ”κΦΤΥψΡήΝΠΘ§ τ”Ύ÷–ΒΒΧβΘ°


 ”°‘ΎΩΈΧΟΟϊ ΠΩΈ ±ΦΤΜ°œΒΝ–¥πΑΗ
”°‘ΎΩΈΧΟΟϊ ΠΩΈ ±ΦΤΜ°œΒΝ–¥πΑΗ ΧλΧλœρ…œΩΈ ±Ά§≤Ϋ―ΒΝΖœΒΝ–¥πΑΗ
ΧλΧλœρ…œΩΈ ±Ά§≤Ϋ―ΒΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{1}{a}ΘΦ\frac{1}{b}$ | BΘ° | a2ΘΦab | CΘ° | a2ΘΦb2 | DΘ° | $\frac{1}{a-b}ΘΦ\frac{1}{a}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δΖ÷±Ί“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
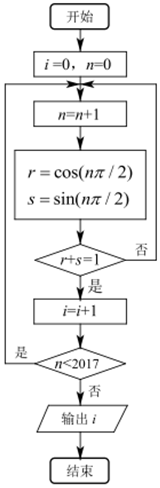 ÷¥––»γΆΦΥυ ΨΒΡ≥Χ–ρΩρΆΦΘ§‘ρ δ≥ωiΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
÷¥––»γΆΦΥυ ΨΒΡ≥Χ–ρΩρΆΦΘ§‘ρ δ≥ωiΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©| AΘ° | 1006 | BΘ° | 1007 | CΘ° | 1008 | DΘ° | 1009 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | a1•dΘΦ0 | BΘ° | |Sn|”–Ήν–Γ÷Β | ||
| CΘ° | ${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$ΘΨ0 | DΘ° | ${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$ΘΨ0 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com