
分析 (1)当t=1时,对f(x)求导,求出函数的最值,即可证明
(2)若t≥1,且f(x)>1在区间[$\frac{1}{e}$,e]上恒成立,即:f(x)在[$\frac{1}{e}$,e]上的最小值大于1;利用导数求判断函数f(x)的最小值.
(3)分类讨论判断g'(x)的单调性与函数的最小值,从而验证g(x)在区间(0,+∞)上单调递增.再构造新函数h(t)=e3t-(2lnt+6),证明h(t)>0,进而判断函数g(x)是否穿过x轴即可.
解答 解:(1)t=1时,f(x)=x-$\frac{1}{x}$-2lnx,x>0
∴f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=$\frac{{x}^{2}-2x+1}{{x}^{2}}$=$\frac{(x-1)^{2}}{{x}^{2}}$≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1-1-0=0,
∴x>1,f(x)>0成立,
(2)依题意,在区间[$\frac{1}{e}$,e]上f(x)min>1,
∵f′(x)=t+$\frac{1}{{x}^{2}}$-$\frac{t+1}{x}$=$\frac{t{x}^{2}-(t+1)x+1}{{x}^{2}}$=$\frac{(tx-1)(x-1)}{{x}^{2}}$,
令f′(x)=0,解得x=1或x=$\frac{1}{t}$≤1,
若t≥e,则由f′(x)>0得,1<x≤e,函数f(x)递增,
由f′(x)<0得,$\frac{1}{e}$≤x<1,函数f(x)递减,
∴f(x)min=f(1)=t-1>1,满足条件,
若1<t<e,则由f′(x)>0得,$\frac{1}{e}$≤x<$\frac{1}{t}$或1<x≤e,函数f(x)递增,
由f′(x)<0得,$\frac{1}{t}$≤x<1,函数f(x)递减,
∴f(x)min=min{f($\frac{1}{e}$),f(1)},
依题意$\left\{\begin{array}{l}{f(\frac{1}{e})>1}\\{f(1)>1}\end{array}\right.$,即$\left\{\begin{array}{l}{t>\frac{{e}^{2}}{e+1}}\\{t>2}\end{array}\right.$,
∴2<t<e,
若t=1,则f′(x)≥0得,函数f(x)在[$\frac{1}{e}$,e]递增,
f(x)min=f($\frac{1}{e}$)<1,不满足条件,
综上所述t>2,
(3)当x∈(0,+∞),g(x)=tx2-(t+1)xlnx+(t+1)x-1
∴g′(x)=2tx-(t+1)lnx,
设m(x)=2tx-(t+1)lnx,
∴m′(x)=2t-$\frac{t+1}{x}$=$\frac{tx-(t+1)}{x}$,
令m′(x)=0,得x=$\frac{t+1}{2t}$,
当0<x<$\frac{t+1}{2t}$时,m'(x)<0;当时x>$\frac{t+1}{2t}$,m'(x)>0.
∴g'(x)在(0,$\frac{t+1}{2t}$)上单调递减,在($\frac{t+1}{2t}$,+∞)上单调递增.
∴g'(x)的最小值为g′($\frac{t+1}{2t}$)=(t+1)(1-ln$\frac{t+1}{2t}$),
∵t>$\frac{1}{e}$,∴$\frac{t+1}{2t}$=$\frac{1}{2}$+$\frac{1}{2t}$<$\frac{1}{2}$+$\frac{e}{2}$<e.
∴g'(x)的最小值g′($\frac{t+1}{2t}$)=(t+1)(1-ln$\frac{t+1}{2t}$)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g($\frac{1}{{e}^{5}{t}^{2}}$)=$\frac{1}{{e}^{10}{t}^{3}}$+$\frac{t+1}{{e}^{5}{t}^{2}}$(6+2lnt)-1,
设h(t)=e3t-(2lnt+6).
则h′(t)=e3-$\frac{2}{t}$.
令h'(t)=0得t=$\frac{2}{{e}^{3}}$.由h'(t)<0,得0<t<$\frac{2}{{e}^{3}}$;
由h'(t)>0,得t>$\frac{2}{{e}^{3}}$.
∴h(t)在(0,$\frac{2}{{e}^{3}}$)上单调递减,在($\frac{2}{{e}^{3}}$,+∞)上单调递增.
∴h(t)min=h($\frac{2}{{e}^{3}}$)=2-2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g($\frac{1}{{e}^{5}{t}^{2}}$)<$\frac{1}{{e}^{7}}$+$\frac{t+1}{{e}^{2}t}$-1=$\frac{1}{{e}^{7}}$+$\frac{1}{{e}^{2}}$+$\frac{1}{{e}^{2}t}$-1<$\frac{1}{{e}^{7}}$+$\frac{1}{{e}^{2}}$+$\frac{1}{e}$-1<0.
又g(1)=2t>0,
∴当t>$\frac{1}{e}$时,函数g(x)恰有1个零点
点评 本题主要考查了利用导数求函数的单调性、函数最值,构造新函数以及函数零点个数等知识点,考查了学生分析问题解决问题的能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{13}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
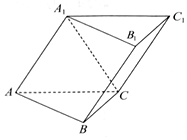 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 9 | B. | -6 27 | C. | -12 9 | D. | -12 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com