
分析 解:(1)通过双曲线x2-y2=2的渐近线方程为y=±x及点到直线的距离公式可知$\frac{|c|}{\sqrt{2}}$=$\sqrt{2}$,结合b=1、a2=b2+c2可求出a,b,c,进而可得椭圆C的方程;
(2)①通过将直线l代入椭圆C方程,利用韦达定理,可得AB的中点S($\frac{-5km}{1+5{k}^{2}}$,$\frac{m}{1+5{k}^{2}}$),利用NS⊥AB即kNS=-$\frac{1}{k}$化简可知5k2+1=4m,代入根的判别式可得结论;②通过设T(x,y),设$\overrightarrow{PA}$=-λ$\overrightarrow{AT}$,$\overrightarrow{PB}$=λ$\overrightarrow{BT}$(λ≠0,±1),可分别用λ、x、y表示出A、B两点的横纵坐标,利用点A、B在椭圆C上整理即得结论.
解答 解:(1)因为双曲线x2-y2=2的渐近线方程为:y=±x,
所以由题可知:b=1,$\frac{|c|}{\sqrt{2}}$=$\sqrt{2}$,a2=b2+c2,
解得:c=2,b=1,a2=5,
所以椭圆C的方程为:$\frac{{x}^{2}}{5}$+y2=1;
(2)①将直线l代入椭圆C得:(1+5k2)x2+10kmx+5m2-5=0,
△=20(1+5k2-m2)>0,设A(x1,y2),B(x2,y2),则
x1+x2=$\frac{-10km}{1+5{k}^{2}}$,x1x2=$\frac{5{m}^{2}-5}{1+5{k}^{2}}$,
则AB的中点S($\frac{-5km}{1+5{k}^{2}}$,$\frac{m}{1+5{k}^{2}}$),
因为NA,NB为邻边的平行四边形为菱形,
所以NS⊥AB,则kNS=-$\frac{1}{k}$,
所以$\frac{\frac{m}{1+5{k}^{2}}+1}{\frac{-5km}{1+5{k}^{2}}}$=$\frac{5{k}^{2}+1+m}{-5km}$=-$\frac{1}{k}$,化简得:5k2+1=4m,
代入△=20(1+5k2-m2)>0,得:-m2+4m>0,解得:0<m<4.
由5k2=4m-1>0得:m>$\frac{1}{4}$,
所以m的取值范围为:($\frac{1}{4}$,4);
②设T(x,y),由题设|$\overrightarrow{PA}$|,|$\overrightarrow{PB}$|,|$\overrightarrow{AT}$|,|$\overrightarrow{TB}$|均不为零,且$\frac{|AP|}{|AT|}$=$\frac{|PB|}{|TB|}$,
又P,A,T,B四点共线,可设$\overrightarrow{PA}$=-λ$\overrightarrow{AT}$,$\overrightarrow{PB}$=λ$\overrightarrow{BT}$(λ≠0,±1),
于是x1=$\frac{1-λx}{1-λ}$,y1=$\frac{1-λy}{1-λ}$,x2=$\frac{1+λx}{1+λ}$,y2=$\frac{1+λx}{1+λ}$,
由于A、B两点在椭圆C上,代入方程,得:
(x2+5y2-5)λ2-2(x+5y-5)λ+1=0,(x2+5y2-5)λ2+2(x+5y-5)λ+1=0,
两式相减,得:4(x+5y-5)λ=0,
由λ≠0可知x+5y-5=0,即点T(x,y)在定直线x+5y-5=0上.
点评 本题是一道直线与圆锥曲线的综合题,涉及求椭圆的方程、定直线问题,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
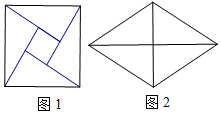 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 16 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com