
分析 数列{an}满足a1=$\frac{1}{256},{a_{n+1}}=2\sqrt{a_n}$,取对数可得:log2an+1=1+$\frac{1}{2}lo{g}_{2}{a}_{n}$.由bn=log2an-2,代入可得:bn+1=$\frac{1}{2}$bn,利用等比数列的通项公式可得:bn=-10×$(\frac{1}{2})^{n-1}$.代入b1•b2•…•bn=(-10)n×$(\frac{1}{2})^{1+2+…+(n-1)}$=(-10)n×${2}^{-\frac{n(n-1)}{2}}$=f(n).作商$\frac{f(n+2)}{f(n)}$=$\frac{100}{{2}^{2n+1}}$,只考虑n为偶数时,即可得出.
解答 解:数列{an}满足a1=$\frac{1}{256},{a_{n+1}}=2\sqrt{a_n}$,
∴log2an+1=1+$\frac{1}{2}lo{g}_{2}{a}_{n}$.
∵bn=log2an-2,
bn+1+2=1+$\frac{1}{2}({b}_{n}+2)$,变形为:bn+1=$\frac{1}{2}$bn,
b1=$lo{g}_{2}\frac{1}{256}$-2=-10.
∴数列{bn}是等比数列,首项为-10,公比为$\frac{1}{2}$.
∴bn=-10×$(\frac{1}{2})^{n-1}$.
则b1•b2•…•bn=(-10)n×$(\frac{1}{2})^{1+2+…+(n-1)}$=(-10)n×${2}^{-\frac{n(n-1)}{2}}$=f(n).
$\frac{f(n+2)}{f(n)}$=$\frac{100}{{2}^{2n+1}}$,只考虑n为偶数时,
n=2时,$\frac{f(4)}{f(2)}$=$\frac{25}{8}$>1.
n=4时,$\frac{f(6)}{f(4)}$=$\frac{25}{128}$<1.
因此f(4)取得最大值.最大值为(-10)4×2-6=$\frac{625}{4}$.
故答案为:$\frac{625}{4}$.
点评 本题考查了等比数列与等差数列的通项公式与求和公式、数列递推关系、作商法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{13}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
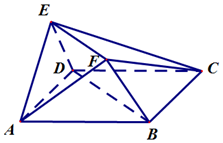 如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD
如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{10}{3}$ | C. | 6 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
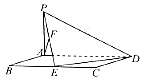 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com