
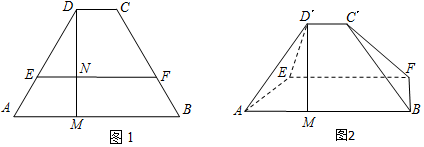
分析 (I)由EF⊥平面D′MN得D′M⊥EF,由勾股定理的逆定理得D′M⊥MN,从而D′M⊥平面ABFE;
(II)根据三角形和相似三角形知识求出各棱长,根据VD′-AEM=VM-AED′列方程解出M到平面AED'的距离.
解答  解:(Ⅰ)∵AB∥CD,EF∥CD,DM⊥AB,
解:(Ⅰ)∵AB∥CD,EF∥CD,DM⊥AB,
∴DM⊥EF,即D'N⊥EF,MN⊥EF,
又D'N∩MN=N,D′M?平面D′MN,D′N?平面D′MN,
∴EF⊥平面MND',又∵D′M?平面D′MN,
∴EF⊥D'M,
∵D′M=2$\sqrt{6}$,D′N=3$\sqrt{3}$,MN=$\sqrt{3}$,
∴D'M2+MN2=D'N2,∴D'M⊥MN,
又MN∩EF=N,MN?平面ABFE,EF?平面ABFE,
∴D'M⊥平面ABFE.
(Ⅱ) 在Rt△ADM中,∵∠A=60°,DN=4$\sqrt{3}$,
∴AM=4,A=8,
∵EF∥AB,∴$\frac{DE}{AE}=\frac{DN}{MN}=3$,
∴DE=6,AE=2,
∴VD′-AEM=$\frac{1}{3}{S}_{△AEM}•D′M$=$\frac{1}{3}×\frac{1}{2}×4×2×sin60°×2\sqrt{6}$=4$\sqrt{2}$,
在Rt△AD′M中,AD′=$\sqrt{A{M}^{2}+D′{M}^{2}}$=2$\sqrt{10}$,
∴D′E2+AE2=AD′2,
∴D'E⊥AE,${S_{△AED'}}=\frac{1}{2}AE•D'E=6$,
设点M到平面AED'的距离为h,
则VM-AED′=$\frac{1}{3}$S△AED′•h=2h,
∴2h=4$\sqrt{2}$,解得$h=2\sqrt{2}$,
∴点M到平面AED'的距离为$2\sqrt{2}$.
点评 本题考查了线面垂直的判定,空间距离计算,棱锥的体积,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
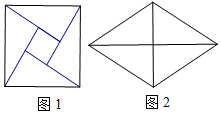 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 513 | C. | 512 | D. | 511 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -250 | B. | 250 | C. | -25 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com