
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
分析 (1)由频率与频数的统计表列出方程组,能求出x、y、z、M的值.
(2)从这M辆纯电动乘用车任选3辆,基本事件总数n=${C}_{10}^{3}$=120,10辆车中,有7辆车续驶里程不低于180公里,选到的3辆车续驶里程都不低于180公里包含的基本事件个数m=${C}_{7}^{3}$=35,由此能求出选到的3辆车续驶里程都不低于180公里的概率.
(3)由题意知X的可能取值为5,6.5,8,8.5,10,12,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)由题意得:$\left\{\begin{array}{l}{\frac{3}{M}=0.3}\\{\frac{6}{M}=x}\\{3+6+y=M}\\{0.3+x+z=1}\end{array}\right.$,
解得x=0.6,y=1,z=0.1,M=10.
(2)从这M辆纯电动乘用车任选3辆,
基本事件总数n=${C}_{10}^{3}$=120,
10辆车中,有7辆车续驶里程不低于180公里,
选到的3辆车续驶里程都不低于180公里包含的基本事件个数m=${C}_{7}^{3}$=35,
∴选到的3辆车续驶里程都不低于180公里的概率p=$\frac{35}{120}$=$\frac{7}{24}$.
(3)由题意知X的可能取值为5,6.5,8,8.5,10,12,
P(X=5)=0.32=0.09,
P(X=6.5)=${C}_{2}^{1}0.3×0.6=0.36$,
P(X=8)=0.62=0.36,
P(X=8.5)=${C}_{2}^{1}0.3×0.1$=0.06,
P(X=10)=${C}_{2}^{1}0.1×0.6=0.12$,
P(X=12)=0.12=0.01,
∴X的分布列为:
| X | 5 | 6.5 | 8 | 8.5 | 10 | 12 |
| P | 0.09 | 0.36 | 0.36 | 0.06 | 0.12 | 0.01 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{13}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
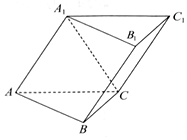 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 9 | B. | -6 27 | C. | -12 9 | D. | -12 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
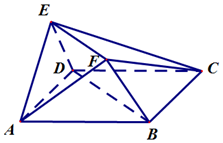 如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD
如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=$\sqrt{2}$EA=$\sqrt{2}$ED,EF∥BD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
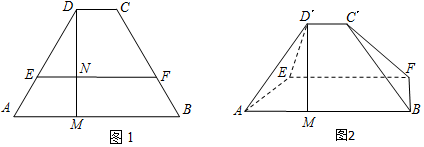
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com