
分析 (Ⅰ)利用等比数列{an}满足an+1+an=9•2n-1,确定数列的公比与首项,即可求数列{an}的通项公式;
(Ⅱ)利用错位相减法求出Sn,再利用不等式Sn>kan+16n-26,分离参数,求最值,即可求实数k的取值范围.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
∵an+1+an=9•2n-1,
∴a2+a1=9,a3+a2=18,
∴q=$\frac{{a}_{3}+{a}_{2}}{{a}_{2}+{a}_{1}}$=$\frac{18}{9}$=2
又2a1+a1=9,∴a1=3.
∴an=3•2n-1. n∈N*.
(Ⅱ)bn=(n-1)an=3(n-1)•2n-1.
∴Sn=3×0×20+3×1×21+…+3(n-2)×2n-2+3(n-1)×2n-1,
∴$\frac{1}{3}$Sn=0×20+1×21+…+(n-2)×2n-2+(n-1)×2n-1,
∴$\frac{2}{3}$Sn=0+1×22+2×23+…+(n-2)×2n-1+(n-1)×2n,
∴-$\frac{1}{3}$Sn=21+22+…+2n-1-(n-1)×2n=$\frac{1-{2}^{n}}{1-2}$-1-(n-1)×2n=(2-n)2n-2,
∴Sn=3(n-2)2n+6,
∵Sn>kan+16n-26,
∴k<$\frac{{S}_{n}-16n+26}{{a}_{n}}$=$\frac{3×(n-2)•{2}^{n}-16n+32}{3×{2}^{n-1}}$=2(n-2)-$\frac{16n-32}{3×{2}^{n-1}}$<2(n-2)(1-$\frac{8}{3•{2}^{n-1}}$)
令f(n)=2(n-2)(1-$\frac{8}{3•{2}^{n-1}}$)
∴f(1)=$\frac{10}{3}$,f(2)=0,
当n≥3时,n-2>0,1-$\frac{8}{3•{2}^{n-1}}$≥1-$\frac{8}{3•{2}^{2}}$=$\frac{1}{3}$>0,
∴f(n)min=f(2)=0,
∴实数k的取值范围为(-∞,0).
点评 本题考查数列递推式,考查等比数列的通项与求和,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
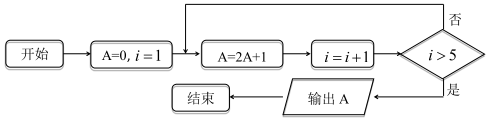
| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
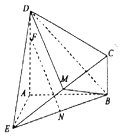 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,6] | B. | [5,7] | C. | [4,6] | D. | [6,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
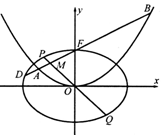 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com