
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)原命题等价于方程xex=x+2在x∈[m,m+1]上有解,由于ex>0,原方程等价于ex-$\frac{2}{x}$-1=0,令r(x)=ex-$\frac{2}{x}$-1,根据函数的单调性求出m的值即可.
解答 解:(Ⅰ)g(x)=axex+ex,∴g′(x)=(ax+a+1)ex,
①a=0时,g′(x)=ex,g′(x)>0在R恒成立,
故函数g(x)在R递增;
②a>0时,x>-$\frac{a+1}{a}$时,g′(x)>0,g(x)递增,
x<-$\frac{a+1}{a}$时,g′(x)<0,函数g(x)递减;
③a<0时,当x>-$\frac{a+1}{a}$时,g′(x)<0,函数g(x)递减,
x<-$\frac{a+1}{a}$时,g′(x)>0,函数g(x)递增,
综上,a=0时,函数g(x)在R递增,
a>0时,函数g(x)在(-∞,-$\frac{a+1}{a}$)递减,在(-$\frac{a+1}{a}$,+∞)递增,
a<0时,函数g(x)在(-∞,-$\frac{a+1}{a}$)递增,在(-$\frac{a+1}{a}$,+∞)递减;
(Ⅱ)由题意得,原命题等价于方程xex=x+2在x∈[m,m+1]上有解,
由于ex>0,故x=0不是方程的解,
故原方程等价于ex-$\frac{2}{x}$-1=0,
令r(x)=ex-$\frac{2}{x}$-1,r′(x)=ex+$\frac{2}{{x}^{2}}$>0对于x∈(-∞,0)∪(0,+∞)恒成立,
故r(x)在(-∞,0)和(0,+∞)递增,
又r(1)=e-3<0,r(2)=e2-2>0,r(-3)=e3-$\frac{1}{3}$<0,r(-2)=e2>0,
故直线y=x+2和曲线y=f(x)的交点有2个,
且两交点的横坐标分别在区间[1,2]和[-3,-2]内,
故整数m的所有值是-3,1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查转化思想,是一道综合题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
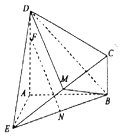 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥查看答案和解析>>
科目:高中数学 来源: 题型:解答题
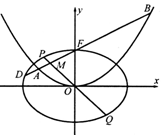 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
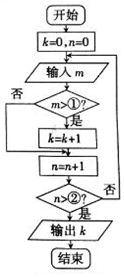 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )| A. | 14,19 | B. | 14,20 | C. | 15,19 | D. | 15,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com