
分析 (1)利用不等式和函数的单调性求出集合A1、A2表示的区间,从而得出结论;
(2)判断fn(m)的单调性,利用不等式的传递性和不等式恒成立得出μ,对m与$\frac{1}{2}$的大小关系进行讨论,判断集合B的有界性;
(3)设c<b<a,对a-b,b-c的大小关系进行讨论,利用不等式的性质得出d与a2+b2+c2的关系,从而得出集合C的上界.
解答 解:(1)y=$\frac{{2}^{x}-1}{{2}^{x}+1}$=1-$\frac{2}{{2}^{x}+1}$<1,
又y=$\frac{{2}^{x}-1}{{2}^{x}+1}$在R上是增函数,且x→-∞时,y→-1,
∴|$\frac{{2}^{x}-1}{{2}^{x}+1}$|<1,
∴A1={y|y=$\frac{{2}^{x}-1}{{2}^{x}+1}$,x∈R}是有界集合,上界为1;
由sinx$>\frac{1}{2}$得2kπ+$\frac{π}{6}$<x<2kπ+$\frac{5π}{6}$,即A2={x|2kπ+$\frac{π}{6}$<x<2kπ+$\frac{5π}{6}$,k∈Z},
∴对任意一个t∈A2,都有一个t1=t+2π∈A2,故A2不是有界集合.
(2)fn(x)-fn-1(x)=fn-12(x)-fn-1(x)+μ=(fn-1(x)-$\frac{1}{2}$)2+μ-$\frac{1}{4}$≥0,
∴fn(x)≥fn-1(x),
又f1(x)=x2+u≥$\frac{1}{4}$,∴fn(x)≥$\frac{1}{4}$,
∵B={fn(m)|n∈N*}为有界集合,∴存在常数M使得fn(m)≤M,
又fn(m)=fn(m)-fn-1(m)+fn-1(m)-fn-2(m)+fn-2(m)+…+f2(m)-f1(m)+f1(m)
=(fn-1(m)-$\frac{1}{2}$)2+μ-$\frac{1}{4}$+(fn-2(m)-$\frac{1}{2}$)2+μ-$\frac{1}{4}$+…+(f1(m)-$\frac{1}{2}$)2+μ-$\frac{1}{4}$+m2+μ
=(fn-1(m)-$\frac{1}{2}$)2+(fn-2(m)-$\frac{1}{2}$)2+…+(f1(m)-$\frac{1}{2}$)2+m2+n(μ-$\frac{1}{4}$)+μ
≥n(μ-$\frac{1}{4}$)+μ,
∴n(μ-$\frac{1}{4}$)+μ≤M恒成立,又μ≥$\frac{1}{4}$,
∴μ=$\frac{1}{4}$,∴f(x)=x2+$\frac{1}{4}$.
设m=$\frac{1}{2}+λ$,
(i)若λ>0,则f1(m)-m=m2+$\frac{1}{4}$-m=($\frac{1}{2}+λ$)2+$\frac{1}{4}$-($\frac{1}{2}+λ$)=λ2>0,
∴f1(m)>m$>\frac{1}{2}$,
∴fn(m)>fn-1(m)>fn-2(m)>…>f2(m)>f1(m)>m$>\frac{1}{2}$,
令g(x)=f(x)-x=(x-$\frac{1}{2}$)2,则g(x)在($\frac{1}{2}$,+∞)上单调递增,
∴f(fn-1(m))-fn-1(m)>f(m)-m=λ2,
即fn(m)>fn-1(m)+λ2>fn-2(m)+2λ2>…>f1(m)+(n-1)λ2=m2+$\frac{1}{4}$+(n-1)λ2.
∵fn(m)≤M恒成立,∴λ2=0,矛盾.
(ii)若λ=0,由(i)可知fn(m)=fn-1(m)=fn-2(m)=…>=f2(m)=f1(m)=m=$\frac{1}{2}$,
显然B={fn(m)|n∈N*}={$\frac{1}{2}$}为有界集合,符合题意;
(iii)若λ<0,同理可得f1(m)-m=m2+$\frac{1}{4}$-m=($\frac{1}{2}+λ$)2+$\frac{1}{4}$-($\frac{1}{2}+λ$)=λ2,
∴f1(m)=m+λ2=$\frac{1}{2}+λ$+λ2,
若f1(m)$>\frac{1}{2}$即$\frac{1}{2}+λ$+λ2$>\frac{1}{2}$,解得λ<-1或λ>0(舍),
由(i)知m不可能大于$\frac{1}{2}$,故λ<-1不成立.
若λ=-1,则m=-$\frac{1}{2}$,fn(m)=fn-1(m)=fn-2(m)=…>=f2(m)=f1(m)=m2+$\frac{1}{4}$=$\frac{1}{2}$,
由(ii)可知符合题意;
若-1<λ<0,则λ2+λ=($λ+\frac{1}{2}$)2-$\frac{1}{4}$∈(-$\frac{1}{4}$,0),
∴f1(m)=m+λ2=$\frac{1}{2}+λ+{λ}^{2}$∈($\frac{1}{4}$,$\frac{1}{2}$),
∴存在λ1∈(-1,0)使得f1(m)=$\frac{1}{2}$+λ1,存在λ2∈(-1,0)使得f2(m)=$\frac{1}{2}$+λ2,
以此类推,存在λn∈(-1,0),使得fn(m)=$\frac{1}{2}+{λ}_{n}$,
此时,$\frac{1}{4}$<f1(m)<f2(m)<f3(m)<…<fn(m)<$\frac{1}{2}$,
显然B═{fn(m)|n∈N*}为有界集合,符合题意.
综上,λ∈[-1,0],∴m的范围是[-$\frac{1}{2}$,$\frac{1}{2}$].
(3)假设c<b<a,
(i)若b=$\frac{a+c}{2}$,则d=($\frac{a-c}{2}$)2,
此时,a2+b2+c2=a2+c2+($\frac{a+c}{2}$)2=(a-c)2+($\frac{a-c}{2}$)2+3ac=5d+3ac,
∴$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$=$\frac{1}{5}$-$\frac{1}{5}$×$\frac{3ac}{{a}^{2}+{b}^{2}+{c}^{2}}$=$\frac{1}{5}$-$\frac{1}{5}$×$\frac{3ac}{{a}^{2}+{c}^{2}+\frac{(a+c)^{2}}{4}}$=$\frac{1}{5}-\frac{1}{5}×$$\frac{12ac}{5{a}^{2}+2ac+5{c}^{2}}$,
而$\frac{12ac}{5{a}^{2}+2ac+5{c}^{2}}$=$\frac{12}{5(\frac{a}{c})^{2}+2+5(\frac{c}{a})^{2}}$∈(0,1),
∴y=$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$=$\frac{1}{5}-\frac{1}{5}×$$\frac{12ac}{5{a}^{2}+2ac+5{c}^{2}}$∈(0,$\frac{1}{5}$).
∴λmin=$\frac{1}{5}$.
(ii)若a-b≥b-c,即a≥2b-c时,d=(b-c)2,
此时5d-(a2+b2+c2)=5(b-c)2-(a2+b2+c2)≤5(b-c)2-(2b-c)2-b2-c2=-6bc+3c2<0,
∴$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$<$\frac{1}{5}$,
(iii)若a-b≤b-c,即0<a<2b-c<2b时,d=(a-b)2,
此时5d-(a2+b2+c2)=5(a-b)2-(a2+b2+c2)=4a2-10ab+4b2-c2=2(a-2b)(2a-b)-c2<0,
∴$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$<$\frac{1}{5}$,
综上,0<y<$\frac{1}{5}$,
∴存在λ=$\frac{1}{5}$,使得λ为有界集合C={y|$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$,a、b、c均为正数}的上界.
点评 本题考查了对新定义的理解与应用,函数最值计算与不等式的应用,分类讨论思想,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得x02-x0+2=0 | |
| B. | 命题“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 在△ABC中,“A=B”是“sinA=sinB”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
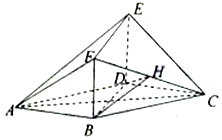 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [$\frac{π}{6}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
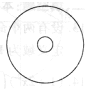 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com