
分析 (I)设单调递增的等差数列{an}的公差为d>0,由3S4=2S5,a5+2是a3,a12的等比中项,可得$3(4{a}_{1}+\frac{4×3}{2}d)$=$2(5{a}_{1}+\frac{5×4}{2}d)$,$({a}_{1}+4d+2)^{2}$=(a1+2d)(a1+11d),联立解得a1,d,即可得出.
(II)由数列{bn}满足$\frac{b_1}{a_1}+\frac{b_2}{a_2}+…+\frac{b_n}{a_n}={3^{n+1}}-3({n∈{N^*}})$,n≥2时,$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n-1}}{{a}_{n-1}}$=3n-3,相减可得:$\frac{{b}_{n}}{{a}_{n}}$=2×3n.
当n=1时,a1=2,b1=12,上式也成立.再利用错位相减法与等比数列的求和公式即可得出.
解答 解:(I)设单调递增的等差数列{an}的公差为d>0,∵3S4=2S5,a5+2是a3,a12的等比中项,
∴$3(4{a}_{1}+\frac{4×3}{2}d)$=$2(5{a}_{1}+\frac{5×4}{2}d)$,$({a}_{1}+4d+2)^{2}$=(a1+2d)(a1+11d),联立解得a1=2=d,
∴an=2+2(n-1)=2n.
(II)由数列{bn}满足$\frac{b_1}{a_1}+\frac{b_2}{a_2}+…+\frac{b_n}{a_n}={3^{n+1}}-3({n∈{N^*}})$,
∴n≥2时,$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n-1}}{{a}_{n-1}}$=3n-3,相减可得:$\frac{{b}_{n}}{{a}_{n}}$=2×3n.
∴bn=4n×3n.
当n=1时,a1=2,b1=2×(32-3)=12,上式也成立.
∴bn=4n×3n.
∴数列{bn}的前n项和Tn=4[3+2×32+…+(n-1)•3n-1+n•3n],
3Tn=4[32+2×33+…+(n-1)•3n+n•3n+1],
∴-2Tn=4(3+32+…+3n-n×3n+1)=4×$[\frac{3({3}^{n}-1)}{3-1}-n×{3}^{n+1}]$,
∴Tn=(2n-1)•3n+1+3.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式求和公式及其性质、错位相减法,考查了推理能力与计算能力,属于中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
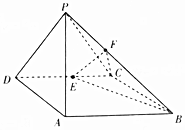 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
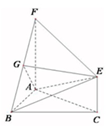 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},+∞})$ | B. | )(0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 30 | 10 | 40 |
| 女生 | 25 | 35 | 60 |
| 合计 | 55 | 45 | 100 |
| P(K2≥k0) | 0.15 | 100. | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 8411. | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com