
分析 (1)设学生甲得分X的所有取值为-15,0,15,30,分别求出相应的概率,由此能求出甲得分X的分布列为和EX.
(2)记事件A:“甲得分不少于15分”,记事件B:“乙得分不少于15分”.甲、乙两人中至少有一人得分大于等于15分的概率为$P=1-P(\bar A•\bar B)=1-(1-P(A))(1-P(B))$.由此能求出结果.
解答 解:(1)设学生甲得分X的所有取值为-15,0,15,30,
$P(X=-15)=\frac{C_6^0C_4^3}{{C_{10}^3}}=\frac{1}{30}$,
$P(X=0)=\frac{C_6^1C_4^2}{{C_{10}^3}}=\frac{3}{10}$,
$P(X=15)=\frac{C_6^2C_4^1}{{C_{10}^3}}=\frac{1}{2}$,
$P(X=30)=\frac{C_6^3C_4^0}{{C_{10}^3}}=\frac{1}{6}$.
∴甲得分X的分布列为
| X | -15 | 0 | 15 | 30 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
点评 本题考查离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
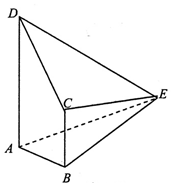 如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.
如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程f(x)=0有两个不相等的整数根 | B. | 方程f(x)=0没有整数根 | ||
| C. | 方程f(x)=0至少有一个整数根 | D. | 方程f(x)=0至多有一个整数根 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com