
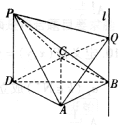
 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.分析 (1)由AC⊥BD,AC⊥PD可得AC⊥平面PBD,故而AC⊥PQ;
(2)计算∠POD的大小判断Q点大体位置,设BQ=x,计算三角形POQ的边长,利用余弦定理解出x;
(3)代入公式V=$\frac{1}{3}{S}_{△POQ}•AC$计算.
解答 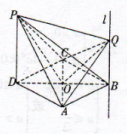 (1)证明:设AC∩BD=O,
(1)证明:设AC∩BD=O,
∵底面ABCD是菱形,∴AC⊥BD,
∵PD⊥平ABCD,AC?平面ABCD,
∴PD⊥AC,又PD?平面PBD,BD?平面PBD,PD∩BD=D,
∴AC⊥平面PBD,
∵BQ∥PD,∴Q∈平面PBD,
∴PQ?平面PBD,
∴AC⊥PQ.
(2)解:连结OP,OQ,
∵△ACD是边长为2的等边三角形,
∴OD=OB=$\sqrt{3}$,∴tan∠POD=$\frac{PD}{OD}=\frac{2}{\sqrt{3}}$$<\sqrt{3}$,
∴∠POD小于60°,
∴Q点位于B点上方,
由(1)知AC⊥平面PDBQ,
∴AC⊥OP,AC⊥OQ,
∴∠POQ为二面角P-AC-D的平面角,
在Rt△POD中,$OP=\sqrt{7}$,设QB=x,则Rt△OBQ中,$OQ=\sqrt{{x^2}+3}$,
在直角梯形PDBQ中,$PQ=\sqrt{{{(2-x)}^2}+{{(2\sqrt{3})}^2}}=\sqrt{{x^2}-4x+16}$,
在△POQ中,由余弦定理得$\sqrt{7({x^2}+3)}=6-4x$,故6-4x>0且3x2-16x+5=0,
解得$x=\frac{1}{3}$,即$QB=\frac{1}{3}$.
(3)解:由(2)知:$OQ=\frac{{2\sqrt{7}}}{3}$,
∴${S_{△POQ}}=\frac{1}{2}×\sqrt{7}×\frac{{2\sqrt{7}}}{3}×sin{120°}=\frac{{7\sqrt{3}}}{6}$,
∵AC⊥面POQ,
∴${V_{Q-ACP}}={V_{A-POQ}}+{V_{C-POQ}}=\frac{1}{3}{S_{△POQ}}•AC=\frac{{7\sqrt{3}}}{9}$.
点评 本题考查了线面垂直的判定,二面角的判断与棱锥的体积计算,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
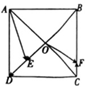 如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )
如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
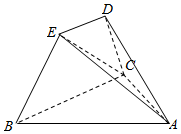 如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
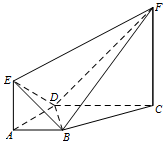 已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.
已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com