
| A. | e2-e+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
分析 二项式(2x+a)5的展开式中,含x2项,利用通项公式求出含有x2的项,可得系数,从而求出a,利用定积分公式求解$\int_1^a{({{e^x}+2x})}dx$即可.
解答 解:二项式(2x+a)5的展开式中,含x2项,
由通项公式${T}_{r+1{=C}_{5}^{r}}{a}^{r}(2x)^{5-r}$,
∵含x2项,
∴r=3.
∴含有x2的项的系数为${C}_{5}^{3}{a}^{3}{2}^{2}$=320,
可得:a=2.
则$\int_1^a{({{e^x}+2x})}dx$=${∫}_{1}^{2}{e}^{x}{d}_{x}+{∫}_{1}^{2}2x{d}_{x}$=e2-e+22-1=e2-e+3.
故选:A.
点评 本题主要考查二项式定理的通项公式的应用,以及定积分公式的计算.属于基础题


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$-1 | B. | 1+$\sqrt{6}$ | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 右程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为24,39,则输出的a=( )
右程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为24,39,则输出的a=( )| A. | 2 | B. | 3 | C. | 4 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
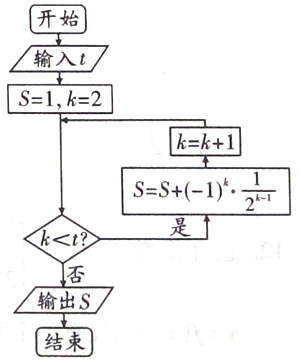
| A. | $\frac{11}{8}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{4}$ | D. | $\frac{21}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com