
【题目】将![]() 这
这![]() 个自然数随机地排列在
个自然数随机地排列在![]() 的正方形方格内,对于同一行或同一列中的任意两个数,计算较大数与较小数的商,得到
的正方形方格内,对于同一行或同一列中的任意两个数,计算较大数与较小数的商,得到![]() 个分数.把最小的分数称之为这种排列的“特征值”.试求特征值的最大值.
个分数.把最小的分数称之为这种排列的“特征值”.试求特征值的最大值.
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
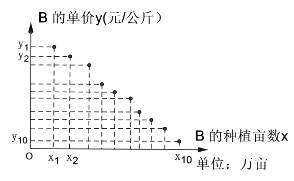
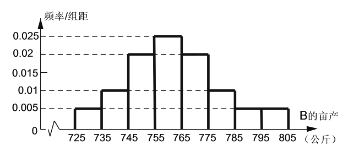
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,今年单价为3.50元/公斤,估计明年单价不变的可能性为10%,变为3.60元/公斤的可能性为60%,变为3.70元/公斤的可能性为30%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
(1)估计明年常规稻A的单价平均值;
(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻B的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻B的亩产超过765公斤的概率;
(3)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出y关于x的线性回归方程;调查得知明年此地杂交稻B的种植亩数预计为2万亩.若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,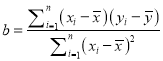 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com