
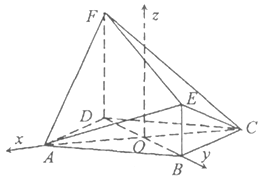
【题目】如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3. 
(1)证明:平面ACF⊥平面BEFD
(2)若二面角A﹣EF﹣C是二面角,求直线AE与平面ABCD所成角的正切值.
【答案】
(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,
∵BE⊥平面ABCD,∴BE⊥AC,
∴AC⊥平面BEFD,
∵AC平面ACF,∴平面ACF⊥平面BEFD
(2)解:设AC与BD的交点为O,由(1)得AC⊥BD,
分别以OA,OB为x轴,y轴,建立空间直角坐标系,
∵BE⊥平面ABCD,∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2﹣(DF﹣BE)2=8,∴BD=2 ![]() .
.
设OA=a,(a>0),
由题设得A(a,0,0),C(﹣a,0,0),E(0, ![]() ),F(0,﹣
),F(0,﹣ ![]() ,2),
,2),
设m=(x,y,z)是平面AEF的法向量,
则  ,取z=2
,取z=2 ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设 ![]() 是平面CEF的一个法向量,
是平面CEF的一个法向量,
则  ,取
,取 ![]() ,得
,得 ![]() =(﹣
=(﹣ ![]() ,1,2
,1,2 ![]() ),
),
∵二面角A﹣EF﹣C是直二面角,
∴ ![]() =﹣
=﹣ ![]() +9=0,解得a=
+9=0,解得a= ![]() ,
,
∵BE⊥平面ABCD,
∴∠BAE是直线AE与平面ABCD所成的角,
∴AB= ![]() =2,∴tan
=2,∴tan ![]() .
.
∴直线AE与平面ABCD所成角的正切值为 ![]() .
.
【解析】(1)推导出AC⊥BD,BE⊥AC,从而AC⊥平面BEFD,由此能证明平面ACF⊥平面BEFD.(2)设AC与BD的交点为O,分别以OA,OB为x轴,y轴,建立空间直角坐标系,利用向量法能求出直线AE与平面ABCD所成角的正切值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x,二次函数g(x)满足g(0)=4,且对任意的x∈R,不等式﹣3x2﹣2x+3≤g(x)≤4x+6成立,则函数f(x)+g(x)的最大值为( )
A.5
B.6
C.4
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P在双曲线 ![]() (a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
(a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
A.± ![]()
B.± ![]()
C.± ![]()
D.± ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcosB,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsinC,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动点P到A,B两点距离之和表示为x的函数f(x),则图像大致为()
BOP=x,将动点P到A,B两点距离之和表示为x的函数f(x),则图像大致为()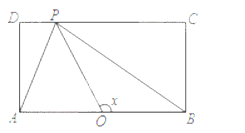
A.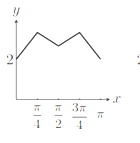
B.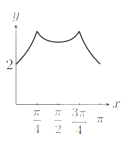
C.
D.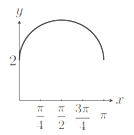
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图O是等腰三角形ABC内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.
(1)(I)证明EF//BC
(2)(II)若AG等于圆O半径,且AE=MN=2![]() ,求四边形EBCF的面积
,求四边形EBCF的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com