
(本小题满分14分)
已知函数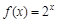 ,
,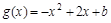
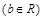 ,记
,记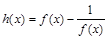 。
。
(Ⅰ)判断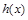 的奇偶性,并证明;
的奇偶性,并证明;
(Ⅱ)对任意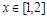 ,都存在
,都存在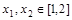 ,使得
,使得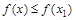 ,
,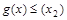 .若
.若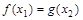 ,求实数
,求实数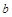 的值;
的值;
(Ⅲ)若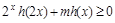 对于一切
对于一切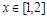 恒成立,求实数
恒成立,求实数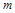 的取值范围.
的取值范围.
(1)奇函数(2) (3)
(3)
解析试题分析:解:(Ⅰ)函数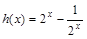 为奇函数………………………………………………2分
为奇函数………………………………………………2分
现证明如下:
∵函数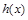 的定义域为
的定义域为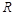 ,关于原点对称。……………………………………3分
,关于原点对称。……………………………………3分
由 …………………5分
…………………5分
∴函数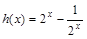 为奇函数…………………………………………………6分
为奇函数…………………………………………………6分
(Ⅱ)据题意知,当 时,
时, ,
,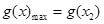 …………7分
…………7分
∵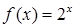 在区间
在区间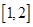 上单调递增,
上单调递增,
∴ ,即
,即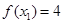 ………………………………………8分
………………………………………8分
又∵
∴函数 的对称轴为
的对称轴为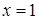
∴函数 在区间
在区间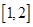 上单调递减
上单调递减
∴ ,即
,即 ………………………………………9分
………………………………………9分
由 ,
,
得 ,∴
,∴ ………………………………………………………………10分
………………………………………………………………10分
(Ⅲ)当 时,
时,
即 ,
,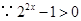 ,
,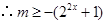 …………………………………………………12分
…………………………………………………12分
令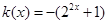 ,
,
下面求函数 的最大值。
的最大值。 ,
,
∴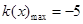 ……………………………………………………………………13分
……………………………………………………………………13分
故 的取值范围是
的取值范围是 ………………………………………………………14分
………………………………………………………14分
考点:本试题考查了函数的奇偶性和单调性的运用。
点评:解决该试题的关键是能熟练的运用指数函数和二次函数的性质得到最值,以及根据奇偶性的定义准确的证明,同时对于不等式的恒成立问题,能分离参数法来得到其取值范围。属于中档题。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
已知函数
 ,
, 为
为 的导数.
的导数.
(1)当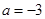 时,求
时,求 的单调区间和极值;
的单调区间和极值;
(2)设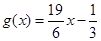 ,是否存在实数
,是否存在实数 ,对于任意的
,对于任意的 ,存在
,存在 ,使得
,使得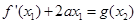 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其他部分都是平地.一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在弧ST上,相邻两边CQ,CR落在正方形的边BC,CD上,求矩形停车场PQCR的面积S的最大值和最小值(结果取整数).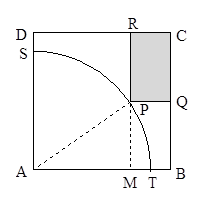
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数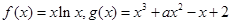
(1)如果函数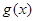 的单调减区间为
的单调减区间为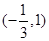 ,求函数
,求函数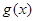 的解析式;
的解析式;
(2)在(1)的条件下,求函数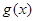 的图像过点
的图像过点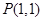 的切线方程;
的切线方程;
(3)证明:对任意的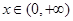 ,不等式
,不等式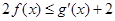 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com