
对于函数 ,若存在区间
,若存在区间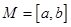 ,使得
,使得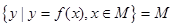 ,则称区间
,则称区间 为函数
为函数 的一个“好区间”.给出下列4个函数:
的一个“好区间”.给出下列4个函数:
①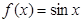 ;②
;②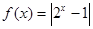 ;③
;③ ;④
;④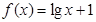 .
.
其中存在“好区间”的函数是 .(填入所有满足条件函数的序号)
②③④
解析试题分析:①函数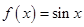 在
在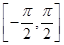 上是单调增函数,若函数在
上是单调增函数,若函数在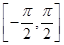 上存“好区间”
上存“好区间”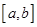 则必有
则必有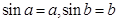 ,即方程
,即方程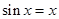 有两个根,令
有两个根,令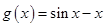
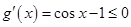
在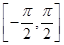 上恒成立,所以函数
上恒成立,所以函数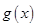 在
在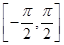 上为减函数,则函数
上为减函数,则函数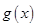 在
在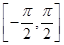 上至多一个零点,即方程
上至多一个零点,即方程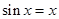 在
在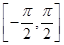 上不可能有两个解,又因为函数
上不可能有两个解,又因为函数 的值域为
的值域为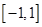 ,所以当
,所以当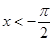 或
或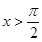 时,方程
时,方程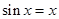 无解.所以函数
无解.所以函数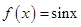 没有“好区间”;
没有“好区间”;
②对于函数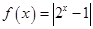 ,该函数在
,该函数在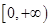 上是增函数由幂函数的性质我们易得,
上是增函数由幂函数的性质我们易得,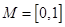 时,
时, ,所以
,所以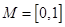 为函数
为函数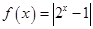 的一个“好区间”.
的一个“好区间”.
③对于函数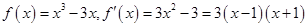 当
当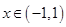 时
时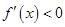 ,所以函数
,所以函数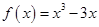 的增区间有
的增区间有 和
和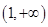 ,减区间是
,减区间是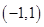 ,取
,取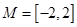 ,此时
,此时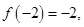
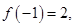
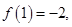
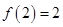 ,所以函数
,所以函数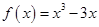 在
在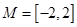 上的值域了是
上的值域了是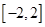 ,则
,则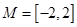 为函数的一个“好区间”;
为函数的一个“好区间”;
④函数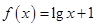 在定义域
在定义域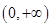 上为增函数,若有“好区间”
上为增函数,若有“好区间”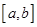
 则
则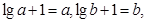 也就是函数
也就是函数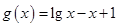 有两个零点,显然
有两个零点,显然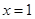 是函数的一个零点,由
是函数的一个零点,由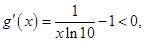
得,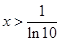 ,函数
,函数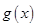 在
在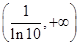 上为减函数;由
上为减函数;由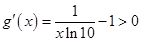 ,得
,得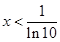 ,函数在
,函数在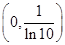 上为增函数.所以
上为增函数.所以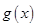 的最大值为
的最大值为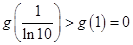 ,则该函数
,则该函数 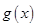 在
在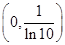 上还有一个零点.所以函数
上还有一个零点.所以函数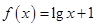 存在“好区间”.
存在“好区间”.
考点:1、函数的单调性;2、函数的零点3、函数的定义域和值域.


科目:高中数学 来源: 题型:填空题
甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程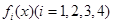 关于时间
关于时间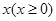 的函数关系式分别为
的函数关系式分别为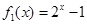 ,
,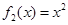 ,
,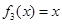 ,
, ,有以下结论:
,有以下结论:
① 当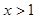 时,甲走在最前面;
时,甲走在最前面;
② 当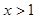 时,乙走在最前面;
时,乙走在最前面;
③ 当 时,丁走在最前面,当
时,丁走在最前面,当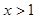 时,丁走在最后面;
时,丁走在最后面;
④ 丙不可能走在最前面,也不可能走在最后面;
⑤ 如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知函数 为
为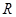 上的偶函数,且对任意
上的偶函数,且对任意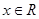 均有
均有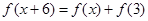 成立且
成立且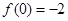 ,当
,当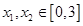 且
且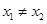 时,有
时,有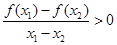 ,给出四个命题:
,给出四个命题:
①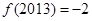 ;
;
②函数 的图像关于
的图像关于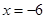 对称;
对称;
③函数 在
在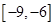 上为增函数;
上为增函数;
④方程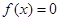 在
在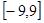 上有4个实根.
上有4个实根.
其中所有正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com