
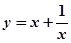 在
在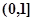 上是减函数,在
上是减函数,在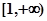 上是增函数;
上是增函数;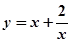 在
在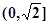 上是减函数,在
上是减函数,在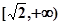 上是增函数;
上是增函数;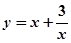 在
在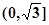 上是减函数,在
上是减函数,在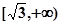 上是增函数;
上是增函数;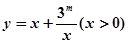 的值域是
的值域是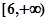 ,则实数
,则实数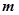 的值是 .
的值是 . 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). 的解析式及其定义域;
的解析式及其定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
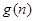 与科技成本的投入次数
与科技成本的投入次数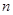 的关系是
的关系是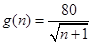 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第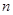 次投入后的年利润为
次投入后的年利润为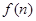 万元.
万元.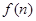 的表达式;
的表达式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
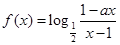 为奇函数,
为奇函数,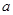 为常数.
为常数.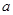 的值;
的值;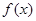 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;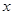 的值,不等式
的值,不等式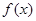 >
>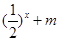 恒成立,求实数
恒成立,求实数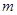 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com