已知函数f(x)=x3+a•x2+bx+c的图象上的一点M(1,m)处的切线的方程为y=2,其中a,b,c∈R.
(1)若a=-3,求f(x)的解析式,并表示成f(x)=(x+t)3+k,(t,k为常数);
(2)问函数y=f(x)是否有单调减区间,若存在,求单调减区间(用a表示),若不存在,请说明理由.
(本小题满分12分)
解:(1)f′(x)=3x
2+2a•x+b?f′(1)=3+2a+b=0
由∵m=2?f(1)=1+a+b+c=2∵a=-3?b=3,c=1,f(x)=x
3-3x
2+3x+1=(x-1)
3+2…(4分)
(2)f′(x)=3x
2+2a•x+b由(1)知b=-2a-3
所以
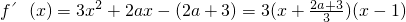
…(6分)
令
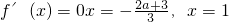
…(8分)
当
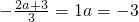
即f′(x)=3(x-1)
2≥0
∵f(x)为R上为增函数,所以函数没有单调减区间; …(9分)
当
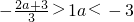
时,可以判定f(x)单调减区间为
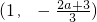
…(10分)
当
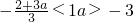
时,可以判定f(x)单调减区间为
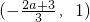
…(11分)
综上:a=-3,函数没有单调减区间;a<-3,f(x)单调减区间为
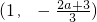
;
a>-3,f(x)单调减区间为
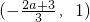
.…(12分)
分析:(1)先求出函数在x=1处的导数,得到切线的斜率,建立一等式,再根据切点在函数图象上,建立另一等式,解方程组即可求出所求;
(2)先求导函数,然后f′(x)=0,讨论两根的大小,将a分为三种情形,再分别求出对应的单调减区间.
点评:本题主要考查了导数的几何意义、利用导数研究函数的单调性,同时考查了分类讨论的思想,属于中档题.

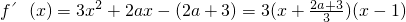 …(6分)
…(6分)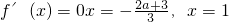 …(8分)
…(8分)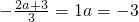 即f′(x)=3(x-1)2≥0
即f′(x)=3(x-1)2≥0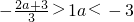 时,可以判定f(x)单调减区间为
时,可以判定f(x)单调减区间为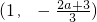 …(10分)
…(10分)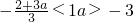 时,可以判定f(x)单调减区间为
时,可以判定f(x)单调减区间为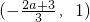 …(11分)
…(11分)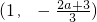 ;
;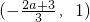 .…(12分)
.…(12分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<