
【题目】给出下列命题:某射手射击一次,击中目标的概率是0.9,他连续射击三次,且他每次射击是否击中目标之间没有影响,有下列结论:①他三次都击中目标的概率是![]() ;②他第三次击中目标的概率是
;②他第三次击中目标的概率是![]() ; ③他恰好2次击中目标的概率是
; ③他恰好2次击中目标的概率是![]() ;④他至少
;④他至少![]() 次击中目标的概率是
次击中目标的概率是![]() ;⑤他至多2次击中目标的概率是
;⑤他至多2次击中目标的概率是![]() .其中正确命题的序号是 ________(正确命题的序号全填上).
.其中正确命题的序号是 ________(正确命题的序号全填上).
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=2BC=2,E为CD中点,以BE为折痕将△BEC折起,使C到C′的位置,且平面BEC′⊥平面ABED.

(1)求证:BC′⊥AE;
(2)求空间四边形ABC′E的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,阅读如图所示的程序框图,若输入的
,阅读如图所示的程序框图,若输入的![]() 的值为
的值为![]() ,输出的
,输出的![]() 的值恰为直线
的值恰为直线![]() 在
在![]() 轴上的截距,且
轴上的截距,且![]() .
.

(1)求直线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)若直线![]() 过直线
过直线![]() 与
与![]() 的交点,且在
的交点,且在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的2倍,求
轴上的截距的2倍,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱椎![]() 中,
中, ![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,底面
,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
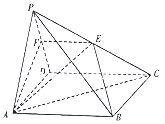
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知距离为![]() 的
的![]() 、
、![]() 两点在直线
两点在直线![]() 的同侧,且
的同侧,且![]() 、
、![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 、
、![]() .问能否作出经过
.问能否作出经过![]() 、
、![]() 两点且与直线
两点且与直线![]() 相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:

(1)根据表中周一到周五的数据,求y关于x的线性回归方程。
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com