
【题目】已知直线![]() ,阅读如图所示的程序框图,若输入的
,阅读如图所示的程序框图,若输入的![]() 的值为
的值为![]() ,输出的
,输出的![]() 的值恰为直线
的值恰为直线![]() 在
在![]() 轴上的截距,且
轴上的截距,且![]() .
.

(1)求直线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)若直线![]() 过直线
过直线![]() 与
与![]() 的交点,且在
的交点,且在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的2倍,求
轴上的截距的2倍,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据程序框图,可得输出的函数![]() ,由输入
,由输入![]() 的值为
的值为![]() 可得直线
可得直线![]() 在
在![]() 轴上的截距.由
轴上的截距.由![]() ,可得直线
,可得直线![]() 的斜率.根据点斜式可得直线
的斜率.根据点斜式可得直线![]() 的方程,联立两直线方程,即可求得交点坐标.
的方程,联立两直线方程,即可求得交点坐标.
(2)讨论截距是否为0:当截距为0时,易得直线方程;当截距不为0时,根据在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的2倍,设出直线方程,代入所过的点,即可求解.
轴上的截距的2倍,设出直线方程,代入所过的点,即可求解.
(1)由程序框图,若输入![]() 的值为
的值为![]() ,由
,由![]()
所以输出![]()
代入可得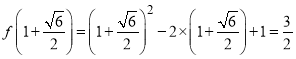
所以![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,
,
∵![]() ,
,
∴![]()
所以![]()
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
联立![]() ,解得
,解得![]() .
.
∴直线![]() 和
和![]() 的交点坐标为
的交点坐标为![]() .
.
(2)当直线![]() 经过原点时,可得方程为
经过原点时,可得方程为![]() .
.
当直线![]() 不经过原点时,设在
不经过原点时,设在![]() 轴上截距为
轴上截距为![]() ,则在
,则在![]() 轴上的截距为
轴上的截距为![]() ,
,
其方程为![]() ,将交点坐标
,将交点坐标![]() 代入可得
代入可得![]() ,解得
,解得![]() ,
,
∴方程为![]() .
.
综上可得直线![]() 方程为
方程为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() .
.
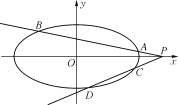
(1) 求椭圆E的标准方程;
(2) 已知P(t,0)为椭圆E外一动点,过点P分别作直线l1和l2,直线l1和l2分别交椭圆E于点A,B和点C,D,且l1和l2的斜率分别为定值k1和k2,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cos ωx·sin![]() +a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(1)求a和ω的值;
(2)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:某射手射击一次,击中目标的概率是0.9,他连续射击三次,且他每次射击是否击中目标之间没有影响,有下列结论:①他三次都击中目标的概率是![]() ;②他第三次击中目标的概率是
;②他第三次击中目标的概率是![]() ; ③他恰好2次击中目标的概率是
; ③他恰好2次击中目标的概率是![]() ;④他至少
;④他至少![]() 次击中目标的概率是
次击中目标的概率是![]() ;⑤他至多2次击中目标的概率是
;⑤他至多2次击中目标的概率是![]() .其中正确命题的序号是 ________(正确命题的序号全填上).
.其中正确命题的序号是 ________(正确命题的序号全填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,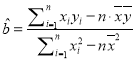 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .
.
(1)若f(x)有两个极值点,求实数m的取值范围:
(2)若函数![]() 有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且
有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com