
(本小题满分10分)
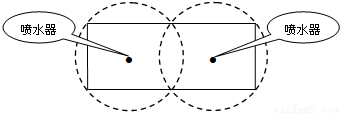
如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器 已知喷水器的喷水区域是半径为5 m的圆 问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
花坛长为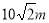 ,宽为
,宽为 ,两喷水器位于矩形分成的两个正方形的中心,则符合要求;
,两喷水器位于矩形分成的两个正方形的中心,则符合要求;
【解析】
试题分析:由题可知,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界,则有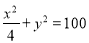
使花坛的面积最大且能全部喷到水,则问题转化为在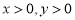 ,
,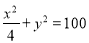 的条件下,求
的条件下,求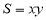 的最大值。此时有两种方法求最值,法一采用的是基本不等式法,法二采用的是二次函数求最值的方法,两种方法求最值,同学们都应该掌握。
的最大值。此时有两种方法求最值,法一采用的是基本不等式法,法二采用的是二次函数求最值的方法,两种方法求最值,同学们都应该掌握。
试题解析:设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界 依题意得: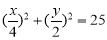 ,(
,(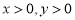 )
)
问题转化为在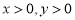 ,
,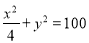 的条件下,求
的条件下,求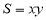 的最大值 4分
的最大值 4分
法一: ,
,
由 和
和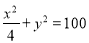 及
及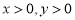 得:
得: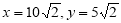
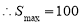
法二:∵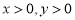 ,
,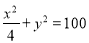 ,
,
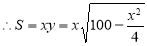 =
=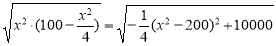
∴当 ,即
,即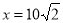 ,
,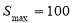
由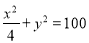 可解得:
可解得: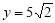 8分
8分
答:花坛的长为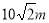 ,宽为
,宽为 ,两喷水器位于矩形分成的两个正方形的中心,则符合要求 10分
,两喷水器位于矩形分成的两个正方形的中心,则符合要求 10分
考点:①利用基本不等式求最值②利用配方法求最值


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年山东省枣庄市高一上学期期中考试数学试卷(解析版) 题型:选择题
方程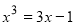 的三根
的三根 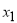 ,
,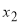 ,
,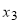 ,其中
,其中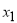 <
<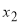 <
<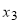 ,则
,则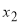 所在的区间为
所在的区间为
A. B.(0 , 1 ) C.(1,
B.(0 , 1 ) C.(1, 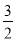 ) D.(
) D.(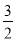 , 2)
, 2)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古赤峰市宁城县高二上学期期末考试文科数学试卷(解析版) 题型:选择题
如图,定点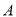 ,
,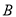 都在平面
都在平面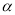 内,定点
内,定点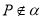 ,
,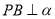 ,
,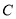 是
是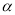 内异于
内异于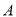 和
和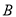 的动点,且
的动点,且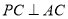 .那么,动点C在平面
.那么,动点C在平面 内的轨迹是( )
内的轨迹是( )
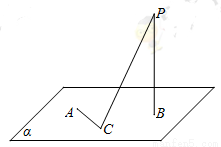
(A) 一条线段,但要去掉两个点 (B) 一个圆,但要去掉两个点
(C) 一个椭圆,但要去掉两个点 (D) 半圆,但要去掉两个点
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市高一上学期期末考试数学试卷(解析版) 题型:填空题
将容量为n的样本中的数据分成6组,绘制频率分布直方图. 若第一组至第六组数据的频率之比为2:3:4:6: 4:1,且前三组数据的频数之和等于36,则n等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com