
分析 (Ⅰ)求出圆的圆心坐标,利用相切列出方程,即可求实数m的值;
(Ⅱ)求出点A的坐标为(2,0),点B的坐标为(0,2),设P点的坐标为(x0,y0),推出点M的坐标为(0,$\frac{2{y}_{0}}{2-{x}_{0}}$),点N的坐标为($\frac{2{x}_{0}}{2-{y}_{0}}$,0),表示出四边形ABNM的面积,利用点P在圆C1上,得x02+y02=4,化简求解即可.
解答 解:(Ⅰ)圆C1的圆心坐标(0,0),半径为$\sqrt{m}$(m>0),
圆C2的圆心坐标(3,4),半径为3,圆心距为:5,
又两圆外切,得$\sqrt{m}+3=5$,解得m=4.
(Ⅱ)由题易得点A的坐标为(2,0),点B的坐标为(0,2),圆C1:x2+y2=4,
设P点的坐标为(x0,y0),x0,y0∈(-2,0).
由题意,得点M的坐标为(0,$\frac{2{y}_{0}}{2-{x}_{0}}$),点N的坐标为($\frac{2{x}_{0}}{2-{y}_{0}}$,0),
四边形ABNM的面积S=$\frac{1}{2}$|AN||BM|=$\frac{1}{2}|2-\frac{2{x}_{0}}{2-{y}_{0}}||2-\frac{2{y}_{0}}{2-{x}_{0}}|$=|$\frac{1}{2}•\frac{4-2{y}_{0}-2{x}_{0}}{2-{y}_{0}}•\frac{4-2{x}_{0}-2{y}_{0}}{2-{x}_{0}}$|=|$\frac{1}{2}•\frac{({4-2{y}_{0}-2{x}_{0})}^{2}}{(2-{y}_{0})(2-{x}_{0})}$|,
由点P在圆C1上,得x02+y02=4,
∴四边形ABNM的面积S=$\frac{4(4-2{x}_{0}-2{y}_{0}+{x}_{0}{y}_{0})}{(2-{y}_{0})(2-{x}_{0})}=4$,
∴四边形ABNM的面积为定值4.
点评 本题考查两个圆的位置关系以及圆的方程的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{36}-\frac{y^2}{16}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{36}=1$ |
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上月考一数学(理)试卷(解析版) 题型:解答题
已知函数 (
(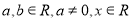 ).
).
(1)若函数 的图象过点
的图象过点 ,函数
,函数 有且只有一个零点,求
有且只有一个零点,求 表达式;
表达式;
(2)在(1)的条件下,当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南八市高二文上月考一数学试卷(解析版) 题型:解答题
在锐角 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com