Question

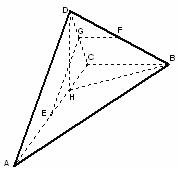
在四面体ABCD中，平面ABC^平面ACD,BC^AC,E、F分别是AC、BD的中点，G是DC上一点且GF//平面ABC。

(1)求证:EG//平面ABD；

(2)求证:平面DCB^平面ACD； 

(3)如果AC=2DC=2BC且∠DAC=30⁰,求BD与平面ABC所成角的余弦值。

Answer 1

证明：（1） GF//平面ABC，GF平面BCD，平面BCD平面ABC=BC

GF//BC，又E、F分别是AC、BD的中点，

G是DC的中点，GE//AD，又GE平面ABD, AD平面ABD,

 EG//平面ABD           

（2）平面ABC^平面ACD ，BC^AC ，

 BC^平面ACD,又DC平面BCD,

平面DCB^平面ACD               

（3）由已知AC=2DC=2BC可设BC=DC=2a(a>0)，则AC=4a,

在△ACD中，∠DAC=30⁰，由正弦定理得 ，

，，

作DH^AC于H，连接BH。

平面ABC^平面ACD ，DH^平面ABC， BH是BD在平面ABC上的射影，

∠DBH是BD与平面ABC的所成角。

在Rt△DCH中，DC=2a，， CH=a，DH=，

在Rt△BCH中，BC=2a，CH=a, BH=，

在Rt△BDH中，DH^BH,DH= BH=，BD=a，

 ，

BD与平面ABC所成角的余弦值为。