考点:棱柱、棱锥、棱台的体积
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)连接A1B,A1B⊥AB1,D1A1⊥AB1.由AB1⊥A1B,AB1⊥D1A1,A1B和D1A1是面A1BD1内的相交直线,所以AB1⊥面A1BD1,又BD1在面A1BD上,AB1⊥BD1,同理,AC⊥BD1.由此能够证明BD1⊥面ACB1.
(2)三棱锥B-ACB1,也就是ABC为底,BB1为高的三棱锥.由此能求出三棱锥B-ACB1体积.
解答:

(1)证明:连接A
1B,在正方体ABCD-A
1B
1C
1D
1中,
面A
1B
1BA是正方形,对角线A
1B⊥AB
1,
在正方体ABCD-A
1B
1C
1D
1中,D
1A
1⊥面A
1B
1BA,AB
1在面A
1B
1BA上,
∴D
1A
1⊥AB
1,
∵AB
1⊥A
1B,AB
1⊥D
1A
1,
A1B和D
1A
1是面A
1BD
1内的相交直线,
∴AB
1⊥面A
1BD
1,又BD
1在面A
1BD
1上,
∴AB
1⊥BD
1,同理,D
1D⊥面ABCD,
AC在面ABCD上,D
1D⊥AC,
在正方形ABCD中对角线AC⊥BD,
∵AC⊥D
1D,AC⊥BD,D
1D和BD是面BDD
1内的相交直线,
∴AC⊥面BDD
1,又BD
1在面BDD
1上,
∴AC⊥BD
1,
∵BD
1⊥AB
1,BD
1⊥AC,
AB
1和AC是面ACB
1内的相交直线
∴BD
1⊥面ACB
1.
(2)解:三棱锥B-ACB
1,也就是ABC为底,BB
1为高的三棱锥,
三棱锥B-ACB
1体积V=
×AB×AD×
BB
1=
×1×(
×1×1)=
. …(12分)
点评:本题考查线面垂直,考查几何体的体积等知识,考查化归与转化的数学思想方法,以及空间想象能力、运算求解能力.

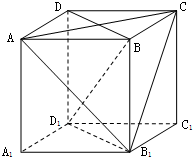 如图,正方体ABCD-A1B1C1D1是棱长为1的正方体.
如图,正方体ABCD-A1B1C1D1是棱长为1的正方体. (1)证明:连接A1B,在正方体ABCD-A1B1C1D1中,
(1)证明:连接A1B,在正方体ABCD-A1B1C1D1中,
