
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上单调增,求
在定义域上单调增,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在定义域上不单调,试判定
在定义域上不单调,试判定![]() 的零点个数,并给出证明过程.
的零点个数,并给出证明过程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)函数
;(3)函数![]() 必有三个不同零点,证明详见解析.
必有三个不同零点,证明详见解析.
【解析】
(1)求导后可得![]() 即为切线斜率,再求出
即为切线斜率,再求出![]() ,利用点斜式即可得解;
,利用点斜式即可得解;
(2)转化条件得![]() 在
在![]() 时恒成立,令
时恒成立,令![]() ,对
,对![]() 求导后求出
求导后求出![]() ,令
,令![]() 即可得解;
即可得解;
(3)由题意若函数![]() 在定义域上不是单调函数
在定义域上不是单调函数![]() ,设
,设![]() ,求导后,即可确定函数
,求导后,即可确定函数![]() 的零点个数,结合
的零点个数,结合![]() 即可得解.
即可得解.
(1)当![]() 时,
时,![]() ,
,
则![]() ,
,![]() ,
,
则在![]() 处的切线斜率为
处的切线斜率为![]() ,
,
所以函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() 即
即![]() ;
;
(2)因为![]() .
.
所以![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
又因为函数![]() 在定义域上为单递增函数,
在定义域上为单递增函数,
所以![]() 在
在![]() 时恒成立,
时恒成立,
即![]() 在
在![]() 时恒成立,
时恒成立,
设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() 在
在![]() 时恒成立
时恒成立![]() ,
,
所以![]() ;
;
(3)因为![]() ,
,
所以![]() ,则
,则![]() 不可能对
不可能对![]() 恒成立,
恒成立,
即![]() 在定义域上不可能始终都为减函数,
在定义域上不可能始终都为减函数,
由(2)知函数![]() 为增函数
为增函数![]() ,
,
所以若函数![]() 在定义域上不是单调函数
在定义域上不是单调函数![]() ,
,
又因为![]() ,所以
,所以![]() 是函数
是函数![]() 一个零点,
一个零点,
令![]() 即
即![]() ,
,
设![]() ,则
,则![]() 与
与![]() 有相同的零点,
有相同的零点,
令![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 有两个不相等实数解
有两个不相等实数解![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以不妨设
,所以不妨设![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
则![]() ,
,![]() ,
,
又因为![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() 在
在![]() 图象不间断,所以
图象不间断,所以![]() 在
在![]() 上有唯一零点;
上有唯一零点;
又因为![]() 在
在![]() 图象不间断,所以
图象不间断,所以![]() 在
在![]() 上有唯一零点;
上有唯一零点;
又因为![]() 是函数
是函数![]() 一个零点,
一个零点,
综上,函数![]() 必有三个不同零点.
必有三个不同零点.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
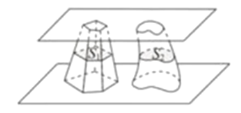
【题目】南北朝时代的伟大数学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面的面积分别为
,被平行于这两个平面的任意平面截得的两个截面的面积分别为![]() ,则“
,则“![]() 总相等”是“
总相等”是“![]() 相等”的( )
相等”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人将编号分别为1,2,3,4,5的5个小球随机放入编号分别为1,2,3,4,5的5个盒子中,每个盒子中放一个小球若球的编号与盒子的编号相同,则视为“放对”,否则视为“放错”,则全部“放错”的情况有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的两个数列![]() ,
,![]() 满足
满足![]() ,
,![]() .且
.且![]() .
.
(1)求证数列![]() 为等差数列;
为等差数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设数列![]() ,
,![]() 的前n项和分别为
的前n项和分别为![]() ,
,![]() ,求使得等式
,求使得等式![]() 成立的有序数对
成立的有序数对![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
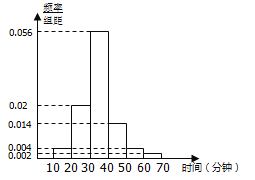
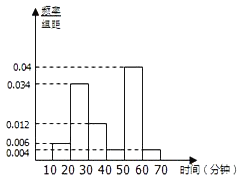
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE.
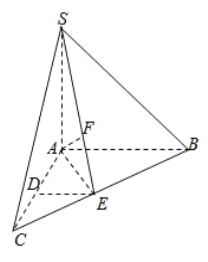
(1)求证:平面SBC⊥平面SAE
(2)若G为DE中点,求二面角G﹣AF﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国南宋数学家杨辉所著的《详解九章算法》一书中,用如图所示的三角形(杨辉三角)解释了二项和的乘方规律.右边的数字三角形可以看作当n依次取0,1,2,3,…时![]() 展开式的二项式系数,相邻两斜线间各数的和组成数列
展开式的二项式系数,相邻两斜线间各数的和组成数列![]() .例:
.例:![]() ,
,![]() ,
,![]() ,….
,….

(1)写出数列![]() 的通项公式(结果用组合数表示),无需证明;
的通项公式(结果用组合数表示),无需证明;
(2)猜想![]() ,与
,与![]() 的大小关系,并用数学归纳法证明.
的大小关系,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com