
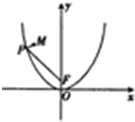
 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$. 分析 设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|MP|+|PD|取得最小,进而可推断出当D,P,M三点共线时|MP|+|PD|最小,答案可得.
解答  解:抛物线C:x2=2y的准线为y=-$\frac{1}{2}$.
解:抛物线C:x2=2y的准线为y=-$\frac{1}{2}$.
设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|,
要求|MP|+|PF|取得最小值,即求|MP|+|PD|取得最小.
当D,P,M三点共线时,|MP|+|PD|最小,为3-(-$\frac{1}{2}$)=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,判断当D,P,M三点共线时,|MP|+|PD|最小是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$) | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$||$\overrightarrow{b}$|+|$\overrightarrow{b}$|2 | ||
| C. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60° | D. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥α,a⊥β,则α∥β | B. | 若a⊥α,b⊥α,则a∥b | C. | 若a?α,b⊥α,则a⊥b | D. | 若a⊥α,α⊥β,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com