
分析 (1)求导数,确定抛物线在A,B两点处的切线的斜率,即可求抛物线在A,B两点处的切线方程;
(2)由$\left\{\begin{array}{l}y=4x-3\\ y=-2x+6\end{array}\right.$得$x=\frac{3}{2}$,利用定积分求由抛物线及其在A,B两点处的切线共同围成的图形的面积.
解答 解:(1)因为y'=-2x+4,
所以抛物线在A,B两点处的切线的斜率分别为4和-2,
其切线方程分别为:y=4x-3和y=-2x+6
(2)由$\left\{\begin{array}{l}y=4x-3\\ y=-2x+6\end{array}\right.$得$x=\frac{3}{2}$
故$S=\int_0^{\frac{3}{2}}{({4x-3+{x^2}-4x+3})}dx+\int_{\frac{3}{2}}^3{({-2x+6+{x^2}-4x+3})}dx$
=$\frac{1}{3}{x^3}\left|\begin{array}{l}\frac{3}{2}\\ 0\end{array}\right.+$$({\frac{1}{3}{x^3}-3{x^2}+9x})\left|\begin{array}{l}3\\ \frac{3}{2}\end{array}\right.$=$\frac{9}{4}$.
点评 本题考查导数的几何意义,考查定积分知识,考查学生分析解决问题的能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
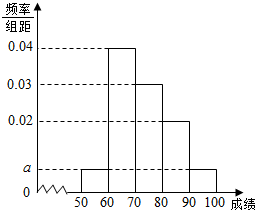 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | y-1=0 | C. | x-y=0 | D. | x+3y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在 | B. | 与x轴平行或重合 | C. | 与x轴垂直 | D. | 与x轴相交不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com