解:(1)证明:∵a
n+1=S
n+1-S
n=

(a
n+1+2)
2-

(a
n+2)
2,
∴8a
n+1=(a
n+1+2)
2-(a
n+2)
2,
∴(a
n+1-2)
2-(a
n+2)
2=0,(a
n+1+a
n)(a
n+1-a
n-4)=0.
∵a
n∈N
*,∴a
n+1+a
n≠0,
∴a
n+1-a
n-4=0.
即a
n+1-a
n=4,∴数列{a
n}是等差数列.
(2)由(1)知a
1=S
1=

(a
1+2),解得a
1=2.∴a
n=4n-2,
b
n=

a
n-30=2n-31,(以下用两种方法求解)
法一:
由b
n=2n-31可得:首项b
1=-29,公差d=2
∴数列{b
n}的前n项和s
n=n
2-30n=(n-15)
2-225
∴当n=15时,s
n=225为最小;
法二:
由
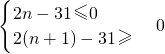
得
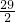
≤n<
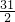
.∵n∈N
*,∴n=15,
∴{a
n}前15项为负值,以后各项均为正值.
∴S
5最小.又b
1=-29,
∴S
15=
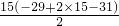
=-225
分析:本题考查数列的通项与其前n项和的关系、等差数列的证明、数列的求和等综合性问题.
(1)根据a
n+1=S
n+1-S
n及前n项和S
n=

(a
n+2)
2,可以得到(a
n+1+a
n)(a
n+1-a
n-4)=0,从而问题得证.
(2)由(1)可得数列{a
n}的通项公式,进而由b
n=

a
n-30得到数列{b
n}的通项公式,然后可求数列{b
n}的前n项和,再由此求其最小值,最小值有两种求法,其一是转化为二次函数的最值,其二是找出正负转折的项.
点评:本题的(2)中求s
n的最值问题是数列中较为常见的一种类型,主要方法有两种:
法一只适用于等差数列的和的最值问题,对于其他数列,因为不能转化为关于n的二次函数,所以无法使用,有一定的局限性;
法二是常规方法,使用范围广,其特点是找到递增或递减的数列中正项和负项的转折“点”而得到答案.

 (an+2)2.
(an+2)2. an-30,求数列{bn}的前n项和的最小值.
an-30,求数列{bn}的前n项和的最小值. (an+1+2)2-
(an+1+2)2- (an+2)2,
(an+2)2, (a1+2),解得a1=2.∴an=4n-2,
(a1+2),解得a1=2.∴an=4n-2, an-30=2n-31,(以下用两种方法求解)
an-30=2n-31,(以下用两种方法求解)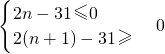 得
得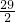 ≤n<
≤n<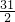 .∵n∈N*,∴n=15,
.∵n∈N*,∴n=15,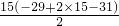 =-225
=-225 (an+2)2,可以得到(an+1+an)(an+1-an-4)=0,从而问题得证.
(an+2)2,可以得到(an+1+an)(an+1-an-4)=0,从而问题得证. an-30得到数列{bn}的通项公式,然后可求数列{bn}的前n项和,再由此求其最小值,最小值有两种求法,其一是转化为二次函数的最值,其二是找出正负转折的项.
an-30得到数列{bn}的通项公式,然后可求数列{bn}的前n项和,再由此求其最小值,最小值有两种求法,其一是转化为二次函数的最值,其二是找出正负转折的项.
