
分析 (1)由ρ=2(0≤θ≤π),得$x_{\;}^2+y_{\;}^2=4\;({y≥0})$.设P(x1,y1),Q(x,y),利用中点坐标公式可得:x1=2x-2,y1=2y,代入$x_1^2+y_1^2=4\;({y≥0})$,即可得出.
(2)轨迹C是一个以(1,0)为圆心,1为半径的半圆,如图所示,设M(1+cosφ,sinφ),设点M处切线l的倾斜角为α由l斜率范围$[{-\sqrt{3},-\frac{{\sqrt{3}}}{3}}]$,可得$\frac{2π}{3}≤α≤\frac{5π}{6}$,由$φ=α-\frac{π}{2}$,$\frac{π}{6}≤φ≤\frac{π}{3}$,即可得出.
解答 解:(1)由ρ=2(0≤θ≤π),得$x_{\;}^2+y_{\;}^2=4\;({y≥0})$.
设P(x1,y1),Q(x,y),
则$x=\frac{{{x_1}+2}}{2},y=\frac{y_1}{2}$,即x1=2x-2,y1=2y,代入$x_1^2+y_1^2=4\;({y≥0})$,
得(2x-2)2+(2y)2=4,∴(x-1)2+y2=1(y≥0).
(Ⅱ)轨迹C是一个以(1,0)为圆心,1为半径的半圆,如图所示,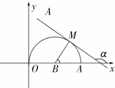
设M(1+cosφ,sinφ),设点M处切线l的倾斜角为α由l斜率范围$[{-\sqrt{3},-\frac{{\sqrt{3}}}{3}}]$,可得$\frac{2π}{3}≤α≤\frac{5π}{6}$,
而$φ=α-\frac{π}{2}$,∴$\frac{π}{6}≤φ≤\frac{π}{3}$,∴$\frac{3}{2}≤1+cosφ≤\frac{{2+\sqrt{3}}}{2}$,
∴点M横坐标的取值范围是$[{\frac{3}{2},\frac{{2+\sqrt{3}}}{2}}]$.
点评 本题考查了极坐标化为直角坐标方程、中点坐标公式、直线与圆的方程、三角函数求值,考查了数形结合方法、推理能力与计算能力,属于中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y与x具有正线性相关关系 | |
| B. | 回归直线必过点($\overline{x}$,$\overline{y}$) | |
| C. | 该女士月收入增加1000元,则其发红包的数量约增加9个 | |
| D. | 该女士月收入为3000元,则可断定其发红包的数量为27个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | k | 3.35 | 5.65 | 8.2 |
| A. | 1 | B. | 0.95 | C. | 0.9 | D. | 0.85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | [4,5] | C. | (4,5) | D. | [4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
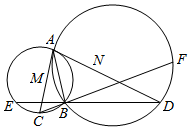 如图,圆M与圆N交于A、B两点,以A为切点作两圆的切线分别交圆M、圆N于C、D两点,延长DB、CB分别交圆M、圆N于E、F.已知DB=10、CB=5.
如图,圆M与圆N交于A、B两点,以A为切点作两圆的切线分别交圆M、圆N于C、D两点,延长DB、CB分别交圆M、圆N于E、F.已知DB=10、CB=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com