
分析 (Ⅰ)由Sn=2an-3,得a1=3,Sn-1=2an-1-3(n≥2),相减可得an=2an-1(n≥2,n∈N),再利用等比数列的通项公式即可得出.
(Ⅱ)利用“错位相减法”、等比数列的求和公式即可得出.
解答 解:(Ⅰ)由Sn=2an-3,①得a1=3,Sn-1=2an-1-3(n≥2),②
①-②,得an=2an-2an-1,即an=2an-1(n≥2,n∈N),
所以数列{an}是以3为首项,2为公比的等比数列,
所以${a_n}=3•{2^{n-1}}$(n∈N*).
(Ⅱ)${T_n}=3(1•{2^0}+2•{2^1}+3•{2^2}+…+n•{2^{n-1}})$,
$2{T_n}=3(1•{2^1}+2•{2^2}+3•{2^3}+…+n•{2^n})$,
作差得$-{T_n}=3(1•{2^0}+1•{2^1}+1•{2^2}+…+1•{2^{n-1}}-n•{2^n})$,
∴${T_n}=3(n-1){2^n}+3$(n∈N*).
点评 本题考查了数列递推关系、等比数列的通项公式及其求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
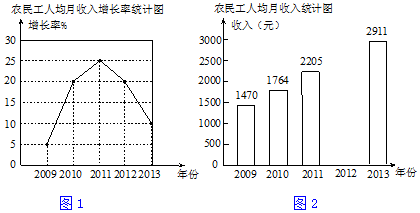
| A. | 2013年农民工人均月收入的增长率是10% | |
| B. | 2011年农民工人均月收入是2205元 | |
| C. | 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了” | |
| D. | 2009年到2013年这五年中2013年农民工人均月收入最高 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com