
���� ������������e=$\frac{\sqrt{2}}{2}$�����᳤Ϊ2���ɵ�a��b������д�����̣�
���ٵ�ֱ��lб�ʲ�����ʱ������ȡA��1��$\frac{\sqrt{2}}{2}$����B��1��-$\frac{\sqrt{2}}{2}$����C��-1��-$\frac{\sqrt{2}}{2}$�������������⣮
�ڵ�ֱ�� lб�ʴ���ʱ����ֱ��AB��y=k��x-1������$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$����� ��2k2+1��x2-4k2x+2k2-2=0����A��x1��y1����B��x2��y2�����ɵ�|AB|=$\sqrt{��1{+k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$2\sqrt{2}\frac{{k}^{2}+1}{2{k}^{2}+1}$
��O��ֱ��kx-y-k=0�ľ���d=$\frac{|k|}{\sqrt{{k}^{2}+1}}$����ABC���Ϊs=$\frac{1}{2}$|AB|��2d=2$\sqrt{2}$��$\frac{\sqrt{{k}^{4}+{k}^{2}}}{2{k}^{2}+1}$=$\frac{\sqrt{6}}{2}$��k=��$\frac{\sqrt{2}}{2}$�����ɵ�ֱ��AB�ķ���
��� �⣺�����������2b=2����b=1��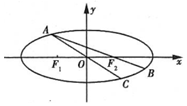
��$\frac{c}{a}=\frac{\sqrt{2}}{1}$��a2=b2+c2����a=$\sqrt{2}$��c=1��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{2}+{y}^{2}=1$��
���ٵ�ֱ��lб�ʲ�����ʱ������ȡA��1��$\frac{\sqrt{2}}{2}$����B��1��-$\frac{\sqrt{2}}{2}$����C��-1��-$\frac{\sqrt{2}}{2}$��
���ABC���ΪS=$\frac{1}{2}��2��\sqrt{2}$=$\sqrt{2}$�����������⣮
�ڵ�ֱ�� lб�ʴ���ʱ����ֱ��AB��y=k��x-1����
��$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$����� ��2k2+1��x2-4k2x+2k2-2=0
��A��x1��y1����B��x2��y2������${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{2{k}^{2}+1}$��${x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{2{k}^{2}+1}$��
��|AB|=$\sqrt{��1{+k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$2\sqrt{2}\frac{{k}^{2}+1}{2{k}^{2}+1}$
�ߵ�O��ֱ��kx-y-k=0�ľ���d=$\frac{|k|}{\sqrt{{k}^{2}+1}}$��
��O���߶�AC���е㣬���C��ֱ��AB�ľ���2d=2��$\frac{|k|}{\sqrt{{k}^{2}+1}}$
���ABC���Ϊs=$\frac{1}{2}$|AB|��2d=2$\sqrt{2}$��$\frac{\sqrt{{k}^{4}+{k}^{2}}}{2{k}^{2}+1}$=$\frac{\sqrt{6}}{2}$��
��4k4+4k2-3=0�����${k}^{2}=\frac{1}{2}$��k=��$\frac{\sqrt{2}}{2}$
��ֱ��AB�ķ���Ϊy=$\frac{\sqrt{2}}{2}$��x-1����y=-$\frac{\sqrt{2}}{2}��x-1��$��
���� ���⿼������Բ�ķ��̣�ֱ������Բ��λ�ù�ϵ�������˵㵽ֱ�ߵľ��빫ʽ��������㣬���������������е��⣮


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
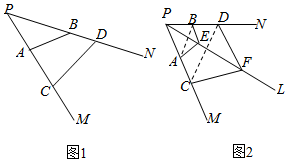 ƽ���ϣ���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬����$\frac{{{S_{��PAB}}}}{{{S_{��PCD}}}}=\frac{PA•PB}{PC•PD}$������S��PAB��S��PCD�ֱ�Ϊ��PAB����PCD����������ռ��У���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬��E��FΪ����PL�ϵ����㣬����$\frac{{{V_{P-ABE}}}}{{{V_{P-CDF}}}}$=$\frac{PA•PB•PE}{PC•PD•PF}$������VP-ABE��VP-CDF�ֱ�Ϊ������P-ABE��P-CDF���������
ƽ���ϣ���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬����$\frac{{{S_{��PAB}}}}{{{S_{��PCD}}}}=\frac{PA•PB}{PC•PD}$������S��PAB��S��PCD�ֱ�Ϊ��PAB����PCD����������ռ��У���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬��E��FΪ����PL�ϵ����㣬����$\frac{{{V_{P-ABE}}}}{{{V_{P-CDF}}}}$=$\frac{PA•PB•PE}{PC•PD•PF}$������VP-ABE��VP-CDF�ֱ�Ϊ������P-ABE��P-CDF����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
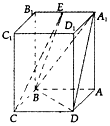 ��������ABCD-A1B1C1D1�У��ı���ABCDΪƽ���ı��Σ�AA1��ƽ��ABCD����BAD=60�㣬AB=2��BC=1��AA1=$\sqrt{6}$��EΪA1B1���е㣮
��������ABCD-A1B1C1D1�У��ı���ABCDΪƽ���ı��Σ�AA1��ƽ��ABCD����BAD=60�㣬AB=2��BC=1��AA1=$\sqrt{6}$��EΪA1B1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|3��x��7}�� | B�� | {x|2��x��10} | C�� | {x|x��2��x��10} | D�� | {x|x��3��x��7} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 8 | C�� | 12 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [3��4�� | B�� | ��-4��-3] | C�� | ��1��3] | D�� | [-3��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
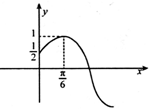 ��֪����$f��x��=Asin��{��x+��}����{A��0���أ�0��0���գ�\frac{��}{2}}��$�IJ���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ�õ�����g��x����ͼ��
��֪����$f��x��=Asin��{��x+��}����{A��0���أ�0��0���գ�\frac{��}{2}}��$�IJ���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ�õ�����g��x����ͼ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com