
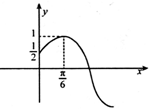
 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.分析 (I)根据图象求出A,ω 和φ,即可求函数f(x)的解析式;通过三角函数的平移规律求出函数g(x)的解析式,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间.
(II)根据(2a-c)cosB-bcosC=0,求出B角的大小,由$f({\frac{A}{2}})=\frac{2}{3}$,求出A的关系式,转化思想求cos(A-B)的值.
解答 解:(I)由图可知A=1,图象过(0,$\frac{1}{2}$)和($\frac{π}{6}$,1)
则有f(0)=sinφ=$\frac{1}{2}$,
∵0<φ$<\frac{π}{2}$,
∴φ=$\frac{π}{6}$
∵f($\frac{π}{6}$)=1,
令$\frac{ωπ}{6}+\frac{π}{6}=\frac{π}{2}$,
可得ω=2,
∴函数f(x)的解析式为:f(x)=sin(2x+$\frac{π}{6}$)
那么g(x)=sin[2(x$-\frac{π}{6}$)x+$\frac{π}{6}$]=sin(2x$-\frac{π}{6}$)
由$-\frac{π}{2}+2kπ≤$2x$-\frac{π}{6}$≤$\frac{π}{2}+2kπ$,k∈Z
得:$-\frac{π}{6}+kπ$≤x≤$\frac{π}{3}+kπ$,
函数g(x)的单调递增区间为[$-\frac{π}{6}+kπ$,$\frac{π}{3}+kπ$],k∈Z;
(II)∵(2a-c)cosB-bcosC=0,即(2a-c)cosB=bcosC
由正弦定理,可得:2sinAcosB-sinCcosB=sinBcosC,
即2sinAcosB=sin(B+C)sinA.
∵sinA≠0
∴2cosB=1,即cosB=$\frac{1}{2}$,
∵0<B<π,
∴B=$\frac{π}{3}$.
由$f({\frac{A}{2}})=\frac{2}{3}$,
可得:sin(A+$\frac{π}{6}$)=$\frac{2}{3}$,
那么求cos(A-B)=cos(A-$\frac{π}{3}$)=sin(A+$\frac{π}{6}$)=$\frac{2}{3}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $12\sqrt{3}$ | C. | $-8\sqrt{3}$ | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.
如图,在长方体ABCD-A1B1C1D1中,$AB=\sqrt{3}AD=\sqrt{3}A{A_1}=\sqrt{3}$,点P为线段A1C上的动点(包含线段端点),则下列结论正确的①②.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | -240 | C. | 60 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com