
| A. | 240 | B. | -240 | C. | 60 | D. | 16 |
分析 画出不等式组$\left\{\begin{array}{l}{x+y≤4}\\{y-2x+2≤0}\\{y≥0}\end{array}\right.$表示的平面区域,求出最优解A(2,2),
计算目标函数n=x+2y的最大值,再利用二项展开式的通项公式求出常数项.
解答 解:画出不等式组$\left\{\begin{array}{l}{x+y≤4}\\{y-2x+2≤0}\\{y≥0}\end{array}\right.$表示的平面区域如图(阴影部分);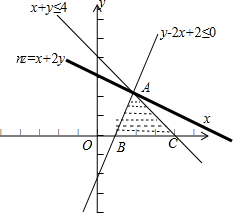
由$\left\{\begin{array}{l}{x+y=4}\\{y-2x+2=0}\end{array}\right.$解得A(2,2),
由可行域知,目标函数n=x+2y在点A(2,2)处取得最大值,
此时n=2+2×2=6,
由${({x-\frac{2}{{\sqrt{x}}}})^6}$的二项展开式的通项公式为
${T_{r+1}}={({-1})^r}C_6^r{2^r}{x^{6-\frac{3}{2}r}}$,
令6-$\frac{3}{2}$r=0,解得r=4;
当r=4时,其常数项为(-1)4•${C}_{6}^{4}$•24=240.
故选:A.
点评 本题考查了线性规划的应用问题,也考查了二项式定理的应用问题,是综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [3,4) | B. | (-4,-3] | C. | (1,3] | D. | [-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
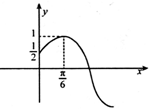 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
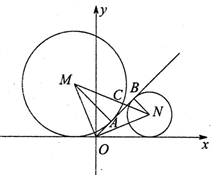 如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=2,φ=π | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | D. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
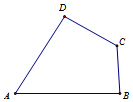 如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.
如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
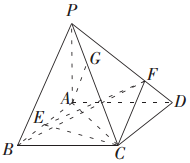 已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com