
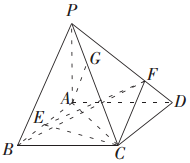
 已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.分析 (Ⅰ)由AB∥CD,AC⊥BA,可得AC⊥CD.由PA⊥底面ABCD,可得PA⊥CD,可得CD⊥平面PAC,即可证明CD⊥AG.
(II)设点F到平面ABCD的距离为d,利用三棱锥的体积计算公式可得:VE-BCF=VF-BEC,可得d,进而得出答案.
解答 (Ⅰ)证明:依题意,因为AB∥CD,AC⊥BA,所以AC⊥CD.
又因为PA⊥底面ABCD,所以PA⊥CD,
因为AC∩PA=A,所以CD⊥平面PAC,
因为AG?平面PAC,所以CD⊥AG.
(Ⅱ)解:设点F到平面ABCD的距离为d,
则${S_{△BEC}}=\frac{1}{2}•BE•BC•sin∠EBC=\frac{1}{2}×\frac{2}{3}×2\sqrt{2}×\frac{{\sqrt{2}}}{2}=\frac{2}{3}$,
由${V_{E-BCF}}={V_{F-BEC}}=\frac{1}{3}{S_{△BEC}}d=\frac{1}{6}$,得$d=\frac{3}{4}$,
故$\frac{FD}{PD}=\frac{d}{PA}=\frac{3}{8}$.
点评 本题考查了线面、面面垂直的判定与性质定理、直角三角形的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | -240 | C. | 60 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (-∞,e] | C. | (-∞,2] | D. | (-∞,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com