
| A. | [-2,2] | B. | (-∞,e] | C. | (-∞,2] | D. | (-∞,1] |
分析 令f(x)=ex-e-x-asinx,分a≤0,0<a≤2,a>2三类讨论,利用导数判断函数的单调性,可判断得:当a≤0时,f(x)>0;当a>0时,f′(x)=ex+e-x-acosx,①0<a≤2,利用导数f′(x)>0⇒f(x)在(0,π)上单调递增,于是f(x)>f(0)=0,满足题意;②若a>2时,令g(x)=ex+e-x-acosx可判断出g(x)=f′(x)=ex+e-x-acosx在(0,$\frac{π}{2}$)上单调递增,x∈(0,x0)时,f′(x)<0,f(x)在(0,x0)上单调递减,于是有f(x)<f(0)=0不满足题意,可得答案.
解答 解:令f(x)=ex-e-x-asinx,
当a≤0时,∵x∈(0,π),∴ex>e-x,sinx>0,∴ex-e-x>0,-asinx≥0,∴f(x)>0;
当a>0时,f′(x)=ex+e-x-acosx,
①若0<a≤2,∵x∈(0,π),∴ex+e-x>2,acosx<a≤2,f′(x)>0,∴f(x)在(0,π)上单调递增,∴f(x)>f(0)=0,满足题意;
②若a>2时,f′(0)=2-a<0,f′($\frac{π}{2}$)>0,∴存在x0∈(0,$\frac{π}{2}$),使得f′(x0)=0.
令g(x)=ex+e-x-acosx,∵g′(x)=ex-e-x+asinx在(0,$\frac{π}{2}$)上单调递增,∴g′(x)>g′(0)=0,
∴g(x)=f′(x)=ex+e-x-acosx在(0,$\frac{π}{2}$)上单调递增,∴x∈(0,x0)时,f′(x)<0,f(x)在(0,x0)上单调递减,
∴f(x)<f(0)=0不满足题意.
综上所述,a∈(-∞,2],
故选:C.
点评 本题考查函数恒成立问题,突出考查分类讨论思想与等价转化思想的综合运用,利用导数判断函数的单调性是难点,属于难题.


科目:高中数学 来源: 题型:解答题
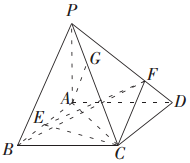 已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
已知四棱锥P-ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2$\sqrt{2}$,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
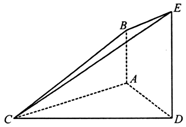 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=-2x+3 | C. | y=-3x+4 | D. | y=x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{5}$,+∞) | B. | [$\frac{1}{5}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x-\sqrt{2}y=0$ | B. | $\sqrt{2}x-y=0$ | C. | $\sqrt{2}x±y=0$ | D. | $x±\sqrt{2}y=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com