
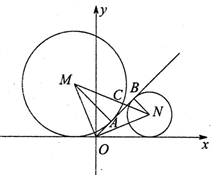
 如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{4}{3}$ |
分析 根据切线的性质可得OM⊥ON,利用相似三角形得出两圆半径比为2:1,在根据三角形相似即可得出tan∠NOX,根据二倍角公式计算k.
解答 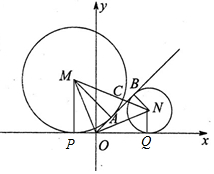 解:过两圆圆心分别作x轴的垂线,垂足分别为P,Q,
解:过两圆圆心分别作x轴的垂线,垂足分别为P,Q,
设圆M,圆N的半径分别为R,r,
∵$\overrightarrow{AC}$=2$\overrightarrow{CB}$,∴AC=2BC.
∵OB是圆M,圆N的垂线,
∴AM⊥OB,BN⊥OB,
∴△MAC∽△NBC,
∴$\frac{AM}{BN}=\frac{AC}{BC}=2$,即R=2r.
∵x轴是两圆的切线,且OB是两圆的切线,
∴OM平分∠BOP,ON平分∠BOQ,
∴∠NOQ+∠POM=90°,
∴∠NOQ=∠PMO,又OM=ON,
∴△MPO≌△OQN,
∴OQ=MP=R,
∴tan∠NOQ=$\frac{NQ}{OQ}$=$\frac{r}{R}$=$\frac{1}{2}$,
∴tan∠BOQ=tan2∠NOQ=$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
∴k=$\frac{4}{3}$.
故选:D.
点评 本题考查了直线与圆的位置关系,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{150}$ | B. | $\frac{2}{752}$ | C. | $\frac{2}{150}$ | D. | $\frac{5}{752}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | -240 | C. | 60 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com