
分析 (1)由2a=2$\sqrt{5}$,根据椭圆的离心率公式即可求得c的值,代入,b2=a2-c2=1,求得椭圆方程,由$\frac{p}{2}$=c,求得c的值,求得抛物线方程;
(2)设直线l的方程,分别代入椭圆方程及抛物线方程,分别求得丨AB丨及丨CD丨,由$\frac{2}{|AB|}$+$\frac{λ}{丨CD丨}$=$\frac{(20+\sqrt{5}λ){k}^{2}+4}{8\sqrt{5}({k}^{2}+1)}$为常数,则须有20+$\sqrt{5}$λ=4,即可求得λ的值.
解答 解:(1)设椭圆的标准方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),由2a=2$\sqrt{5}$,则a=$\sqrt{5}$,离心率为e=$\frac{c}{a}$=$\frac{2\sqrt{5}}{5}$,
则c=2,b2=a2-c2=1,
故椭圆E的方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$;…4分
由$\frac{p}{2}$=c,解得:c=4,
故抛物线G的方程为y2=8x;…5分
(2)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由题意,直线l的方程为y=k(x-2)(k≠0),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{5}+{y}^{2}=1}\\{y=k(x-2)}\end{array}\right.$,消去y,整理得(1+5k2)x2-20k2x+20k2-5=0,…(6分)
△1=400k4-4(20k2-5)(1+5k2)=20(k2+1)>0. …(7分)
|AB|=$\sqrt{1+{k}^{2}}$|x2-x1|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{5}(1+{k}^{2})}{1+5{k}^{2}}$. …(8分)
由 $\left\{\begin{array}{l}{{y}^{2}=8x}\\{y=k(x-2)}\end{array}\right.$,消去y,整理得k2x2-(4k2+8)x+4k2=0,…(9分)
△2=(4k2+8)2-4k2•4k2=64(k2+1)>0,
则x3+x4=$\frac{4{k}^{2}+8}{{k}^{2}}$,
由抛物线定义得|CD|=x3+x4+4=$\frac{8({k}^{2}+1)}{{k}^{2}}$,…(10分)
∴$\frac{2}{|AB|}$+$\frac{λ}{丨CD丨}$=$\frac{1+5{k}^{2}}{2\sqrt{5}({k}^{2}+1)}$+$\frac{λ{k}^{2}}{8({k}^{2}+1)}$=$\frac{(20+\sqrt{5}λ){k}^{2}+4}{8\sqrt{5}({k}^{2}+1)}$,…(11分)
要使$\frac{2}{|AB|}$+$\frac{λ}{丨CD丨}$为常数,则须有20+$\sqrt{5}$λ=4,
解得λ=-$\frac{16\sqrt{5}}{5}$. …(12分)
∴存在λ=-$\frac{16\sqrt{5}}{5}$,使$\frac{2}{|AB|}$+$\frac{λ}{丨CD丨}$为常数.
点评 本题考查圆锥曲线的综合应用,椭圆与抛物线的位置关系的应用,考查转化思想以及计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
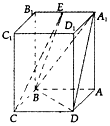 在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1=$\sqrt{6}$,E为A1B1的中点.
在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1=$\sqrt{6}$,E为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,4) | B. | (-4,-3] | C. | (1,3] | D. | [-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,0) | C. | (0,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})∪({2{e^{\frac{3}{2}}},+∞})$ | B. | $({-∞,\frac{1}{2}})∪({4{e^{\frac{3}{2}}},+∞})$ | C. | $({-∞,2{e^{\frac{3}{2}}}})$ | D. | $({-∞,1})∪({4{e^{\frac{3}{2}}},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
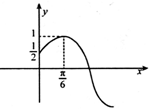 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
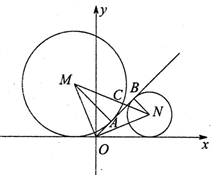 如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
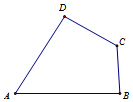 如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.
如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com