
| A. | $({0,\frac{1}{2}})∪({2{e^{\frac{3}{2}}},+∞})$ | B. | $({-∞,\frac{1}{2}})∪({4{e^{\frac{3}{2}}},+∞})$ | C. | $({-∞,2{e^{\frac{3}{2}}}})$ | D. | $({-∞,1})∪({4{e^{\frac{3}{2}}},+∞})$ |
分析 由题意可知:求导,y=ex(2x-1)与y=2a(x-1)有两个交点,设切点坐标,根据直线的斜率公式及导数的几何意义,即可求得切点,代入根据函数函数的单调性即可求得求得a的取值范围.
解答 解:函数f(x)=ex(2x-3)-ax2+2ax+b,求导f′(x)=ex(2x-1)-2ax+2a,
由题意可知函数 f(x)存在两个极值点x1,x2,则y=ex(2x-1)与y=2a(x-1)有两个交点,
则设切点(x0,${e}^{{x}_{0}}$(2x0-1)),y=2a(x-1)恒过点(1,0)
求导y′=ex(2x+1),令y′>0时,解得x>-$\frac{1}{2}$,当y′<0,解得x<-$\frac{1}{2}$,
∴y=ex(2x-1)在(-∞,-$\frac{1}{2}$)单调递减,在(-$\frac{1}{2}$,+∞)单调递增;
则y=ex(2x-1)在(x0,${e}^{{x}_{0}}$(2x0-1))处的切线斜率k=${e}^{{x}_{0}}$(2x0+1),
则${e}^{{x}_{0}}$(2x0+1)=$\frac{{e}^{{x}_{0}}(2{x}_{0}-1)}{{x}_{0}-1}$,整理得:2x02-3x0=1,解得:x0=0,或x0=$\frac{3}{2}$,
∴当x0=0时,则k=1,即2a=1,a=$\frac{1}{2}$,
x0=$\frac{3}{2}$,则k=4${e}^{\frac{3}{2}}$,2a=4${e}^{\frac{3}{2}}$,a=2${e}^{\frac{3}{2}}$,
要使y=ex(2x-1)与y=2a(x-1)有两个交点,
则0<a<$\frac{1}{2}$或a>2${e}^{\frac{3}{2}}$,
当0<a<$\frac{1}{2}$,f′(x)=0,则y=ex(2x-1)与y=2a(x-1)有两个交点x1,x2,
令由函数图象可知(-∞,x2)单调递增,在(x2,x1)单调递减,在(x1,+∞)单调递增,
则当x=x2时,取极大值,当x=x1取极小值,且x2<x1,
满足极小值点x1大于极大值点x2,
同理可知:极小值点x1大于极大值点x2,
∴实数a的取值范围(0,$\frac{1}{2}$)∪(2${e}^{\frac{3}{2}}$,+∞),
另解:取a=0代入可知不合题意,f(x)=ex(2x-3)+b的导数为f′(x)=ex(2x-1),
只有极小值,无极大值.
则BCD三项均不合,
故选A.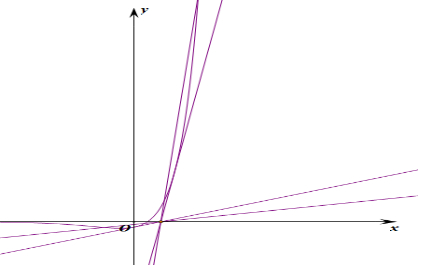
点评 本题考查导数的综合应用,考查导数与函数单调性及极值的关系,导数的几何意义,考查数形结合思想,属于难题.


科目:高中数学 来源: 题型:选择题
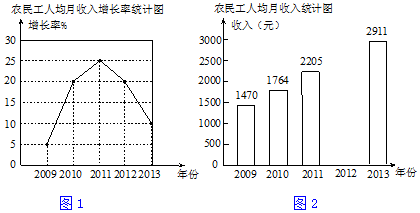
| A. | 2013年农民工人均月收入的增长率是10% | |
| B. | 2011年农民工人均月收入是2205元 | |
| C. | 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了” | |
| D. | 2009年到2013年这五年中2013年农民工人均月收入最高 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{150}$ | B. | $\frac{2}{752}$ | C. | $\frac{2}{150}$ | D. | $\frac{5}{752}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com