Question

18．某学校门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，若都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以2秒为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过1秒的概率是（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{2}$
• C． $\frac{3}{4}$
• D． $\frac{7}{8}$

Answer 1

分析 设这两串彩灯在第一次闪亮时的时间分别为x，y，则$\left\{\begin{array}{l}{0＜x＜2}\\{0＜y＜2}\\{|x-y|≤1}\end{array}\right.$，作出这个不等式组表示的区域，由几何概型的概率公式能求出它们第一次闪亮的时刻相差不超过1秒的概率．

解答 设这两串彩灯在第一次闪亮时的时间分别为x，y，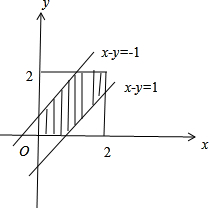
则$\left\{\begin{array}{l}{0＜x＜2}\\{0＜y＜2}\\{|x-y|≤1}\end{array}\right.$，
作出这个不等式组表示的区域，如图：
由几何概型的概率公式得：
它们第一次闪亮的时刻相差不超过1秒的概率：
p=$\frac{{2}^{2}-2（\frac{1}{2}×1×1）}{{2}^{2}}$=$\frac{3}{4}$．
故选：C．

点评 本题考查概率的求法，考查不等式组表示的区域、几何概型等基础知识，考查推理论证能力、运算求解能力，考查数形结合思想、化归与转化思想，是中档题．