
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
分析 设过AB作互相垂直的两个平面α、β截该球所得的两个截面圆分别为圆O1,O2,半径分别为r1,r2,球半径为R,
则有$\left\{\begin{array}{l}{{R}^{2}=O{{O}_{1}}^{2}+{{r}_{1}}^{2}}\\{{R}^{2}=O{{O}_{2}}^{2}+{{r}_{2}}^{2}}\end{array}\right.$,⇒$O{{O}_{1}}^{2}+O{{O}_{2}}^{2}=2{R}^{2}-(O{{O}_{1}}^{2}+O{{O}_{2}}^{2}$)
由$π{{r}_{1}}^{2}+π{{r}_{2}}^{2}=16π$⇒${{r}_{1}}^{2}+{{r}_{2}}^{2}=16$
由OH2=$O{{O}_{1}}^{2}+O{{O}_{2}}^{2}$=8,得AB=2$\sqrt{{R}^{2}-O{H}^{2}}=4$
解答 解:如图所示:设过AB作互相垂直的两个平面α、β截该球所得的两个截面圆分别为圆O1,O2,半径分别为r1,r2,球半径为R,
则有$\left\{\begin{array}{l}{{R}^{2}=O{{O}_{1}}^{2}+{{r}_{1}}^{2}}\\{{R}^{2}=O{{O}_{2}}^{2}+{{r}_{2}}^{2}}\end{array}\right.$,⇒$O{{O}_{1}}^{2}+O{{O}_{2}}^{2}=2{R}^{2}-({{r}_{1}}^{2}+{{r}_{2}}^{2})$
又因为α,β截该球所得的两个截面的面积之和为16π,∴$π{{r}_{1}}^{2}+π{{r}_{2}}^{2}=16π$⇒${{r}_{1}}^{2}+{{r}_{2}}^{2}=16$
∴,$O{{O}_{1}}^{2}+O{{O}_{2}}^{2}=2{R}^{2}-({{r}_{1}}^{2}+{{r}_{2}}^{2})$=2×$(2\sqrt{3})^{2}-16=8$.
∵OH2=$O{{O}_{1}}^{2}+O{{O}_{2}}^{2}$=8,∴AB=2$\sqrt{{R}^{2}-O{H}^{2}}=4$
故选:D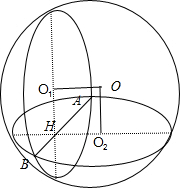
点评 本题考查了球的性质,把空间问题转化为平面问题是解题的关键,属于中档题,


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{150}$ | B. | $\frac{2}{752}$ | C. | $\frac{2}{150}$ | D. | $\frac{5}{752}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f'(m)<0,f'(n)<0 | B. | f'(m)>0,f'(n)>0 | C. | f'(m)<0,f'(n)>0 | D. | f'(m)>0,f'(n)<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com